题目内容
11.已知函数f(x)=$\frac{x}{x+2}$-ax2,其中a∈R.(1)若a=1时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点.
分析 (1)当a=1时,函数f(x)=$\frac{x}{x+2}$-x2,令$\frac{x}{x+2}$-x2=0,可得函数f(x)的零点.
(2)当a>0时,若x>0,由函数f(x)=0得:ax2+2ax-1=0,进而可证得f(x)在(0,+∞)上有唯一零点.
解答 解:(1)当a=1时,函数f(x)=$\frac{x}{x+2}$-x2,
令$\frac{x}{x+2}$-x2=0,可得可得 x=0,或x2+2x-1=0,
解得 x=0,或x=-1-$\sqrt{2}$,或x=-1+$\sqrt{2}$.
综上可得,当a=1时,函数f(x)的零点为 x=0,或x=-1-$\sqrt{2}$,或x=-1+$\sqrt{2}$
(2)证明:∵当a>0时,x>0,由函数f(x)=0得:ax2+2ax-1=0,
记g(x)=ax2+2ax-1,
则g(x)的图象是开口朝上的抛物线,
由g(0)=-1<0得:
函数g(x)在(0,+∞)内有且仅有一个零点.
∴函数f(x)在(0,+∞)上有唯一零点
点评 本题主要考查函数的零点与方程的根的关系,转化思想,二次函数的图象和性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.甲、乙两人玩一种游戏,游戏规则如下:先将筹码放在如下表的正中间D处,投掷一枚质地均匀的硬币,若正面朝上,筹码向右移动一格;若反面朝上,筹码向左移动一格.
(1)将硬币连续投掷三次,现约定:若筹码停在A或B或C或D处,则甲赢;否则,乙赢.问该约定对乙公平吗?请说明理由.
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定:
①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A-G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.
| A | B | C | D | E | F | G |
| 30 | 5 | 10 | 10 | 5 | 20 | 30 |
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定:
①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A-G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.
2.设U=R,A={x|2x<2},B={x|log2x<0},则A∩(∁UB)=( )
| A. | ∅ | B. | {x|x≤0} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
19.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )


| A. | f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)在[-$\frac{π}{3}$,0]上单调递增 | |
| C. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| D. | 将函数y=2sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{6}$个单位得到f(x)的图象 |
16.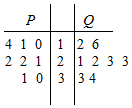 从某工厂生产的P,Q两种型号的玻璃种分别随机抽取8个样品进行检查,对其硬度系数进行统计,统计数据用茎叶图表示(如图所示),则P组数据的众数和Q组数据的中位数分别为( )
从某工厂生产的P,Q两种型号的玻璃种分别随机抽取8个样品进行检查,对其硬度系数进行统计,统计数据用茎叶图表示(如图所示),则P组数据的众数和Q组数据的中位数分别为( )
 从某工厂生产的P,Q两种型号的玻璃种分别随机抽取8个样品进行检查,对其硬度系数进行统计,统计数据用茎叶图表示(如图所示),则P组数据的众数和Q组数据的中位数分别为( )
从某工厂生产的P,Q两种型号的玻璃种分别随机抽取8个样品进行检查,对其硬度系数进行统计,统计数据用茎叶图表示(如图所示),则P组数据的众数和Q组数据的中位数分别为( )| A. | 22和22.5 | B. | 21.5和23 | C. | 22和22 | D. | 21.5和22.5 |
3.甲乙两位同学进行乒乓球比赛,甲获胜的概率为0.4,现采用随机模拟的方法估计这两位同学打3局比赛甲恰好获胜2局的概率:先利用计算器产生0到9之间取整数值的随机数,制定1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每三个随机数为一组,代表3局比赛的结果,经随机模拟产生了30组随机数
102 231 146 027 590 763 245 207 310 386 350 481 337 286 139
579 684 487 370 175 772 235 246 487 569 047 008 341 287 114
据此估计,这两位同学打3局比赛甲恰好获胜2局的概率为( )
102 231 146 027 590 763 245 207 310 386 350 481 337 286 139
579 684 487 370 175 772 235 246 487 569 047 008 341 287 114
据此估计,这两位同学打3局比赛甲恰好获胜2局的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{11}{30}$ |