��Ŀ����
1�����������⣺��y=|sinx-$\frac{1}{2}$|�������ǦУ�
��y=sinx+sin|x|��ֵ����[0��2]��
�۷���cosx=lgx�����⣻
�ܦ�Ϊ��ʵ����y=2sin��x��$[-\frac{��}{3}��\frac{2��}{3}]$�ϵ�������ô�ص�ȡֵ��Χ��$��0��\frac{3}{4}]$��
����y=3sin��2x+$\frac{��}{4}$���У���f��x1��=f��x2��=0����x1-x2��Ϊ�е���������
����A��B����ǡ�ABC�������ڽǣ����P��cosB-sinA��sinB-cosA�ڵڶ����ޣ�
���ڡ�ABC�У���$\overrightarrow{AB}•\overrightarrow{BC}��0$�����ABC�۽������Σ��������������Ϊ��������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
���� �٣���y=|sin����x-$\frac{1}{2}$|��������$\frac{��}{��}$����
�ڣ���x��0ʱ��y=sinx+sin|x|=2sinxֵ����[0��2]����
�ۣ���lg2�У�1��lg4�У�1������cosx=lgx�����⣬��ȷ��
�ܣ���Ϊ��ʵ����y=2sin��x��$[-\frac{��}{3}��\frac{2��}{3}]$�ϵ������������������Һ����ĵ����Կɵæ�•$\frac{2��}{3}��\frac{��}{2}$�ܣ��ɴ���������صķ�Χ��$��0��\frac{3}{4}]$����
�ݣ�����������T=�У�����ֵ����0��x֮�����СֵΪ$\frac{T}{2}$������x1-x2����$\frac{��}{2}$����������
�ޣ���A��B����ǡ�ABC�������ڽǣ�$\frac{��}{2}��\\;B��\frac{��}{2}-A$B��$\frac{��}{2}$-A���� cosB-sinA��0��sinB-cosA��0����
��� �⣺���ڢ٣���y=|sin����x-$\frac{1}{2}$|��������$\frac{��}{��}$������ȷ��
���ڢڣ���x��0ʱ��y=sinx+sin|x|=2sinxֵ����[0��2]���ʴ���
���ڢۣ���lg2�У�1��lg4�У�1������cosx=lgx�����⣬��ȷ��
���ڢܣ���Ϊ��ʵ����y=2sin��x��$[-\frac{��}{3}��\frac{2��}{3}]$�ϵ������������������Һ����ĵ����Կɵæ�•$\frac{2��}{3}��\frac{��}{2}$�ܣ��ɴ���������صķ�Χ��$��0��\frac{3}{4}]$������ȷ��
���ڢݣ�����������T=�У�����ֵ����0��x֮�����СֵΪ$\frac{T}{2}$������x1-x2����$\frac{��}{2}$�����������ʴ���
���ڢޣ���A��B����ǡ�ABC�������ڽǣ�$\frac{��}{2}��\\;B��\frac{��}{2}-A$B��$\frac{��}{2}$-A���� cosB-sinA��0��sinB-cosA��0������ȷ��
��ѡ��C��
���� ���⿼�����������٣��漰�����Ǻ�����֪ʶ�����ڻ����⣮

| A�� | 22016 | B�� | 22018 | C�� | -22017 | D�� | 22017 |
| �·� | 1 | 2 | 3 | 4 | 5 | 6 |
| ������x������� | 10 | 11 | 13 | 12 | 8 | 6 |
| ����y����Ԫ�� | 22 | 25 | 29 | 26 | 16 | 12 |
��2�����ɻع�ֱ�߷��̵õ��Ĺ���������ʣ�µļ������ݵ�����������2��Ԫ������Ϊ�õ��Ļع�ֱ�߷���������ģ��������ûع�ֱ�߷����Ƿ����룿
���ο���ʽ��$\widehat{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$��=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��$\widehat{a}$=$\overline{y}$-b$\overline{x}$��
| A�� | $\frac{1}{2}$ | B�� | $-\frac{1}{2}$ | C�� | $\frac{{\sqrt{3}}}{2}$ | D�� | $-\frac{{\sqrt{3}}}{2}$ |
| A�� | $\frac{1}{2}$ | B�� | $-\frac{1}{2}$ | C�� | $\frac{{\sqrt{3}}}{2}$ | D�� | -1 |
| A�� | $\sqrt{5}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | $\sqrt{5}$��$\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{5}}{2}$ |
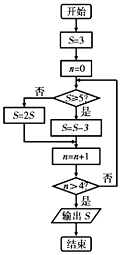
| A�� | 3 | B�� | 4 | C�� | 6 | D�� | 7 |