题目内容
a、b为实数,则下列不等式中成立的是( )
A、a>b,则
| ||||
B、a<b,则
| ||||
C、
| ||||
D、
|
考点:不等式的基本性质
专题:不等式的解法及应用
分析:本题可根据不等式的基本性质进行化简变形,从而判断出选项是否正确,得到本题结论.
解答:
解:选项A,当a>b时,取a=1,b=-1,
=1,
=-1,
>
,故
<
不成立,选项A不正确;
选项B,当a<b时,取a=-1,b=1,
=-1,
=1,
<
,故
>
不成立,选项B不正确;
选项C,当
>
>0时,有:a>0,b>0,∴
×ab>
×ab,∴b>a,故选项C正确;
选项D与C矛盾,故不成立.
故选C.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
选项B,当a<b时,取a=-1,b=1,
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
选项C,当
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
选项D与C矛盾,故不成立.
故选C.
点评:本题考查的是不等式基本性质,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=a(x-
)-2lnx(a∈R),g(x)=-
,若至少存在一个x0∈[1,e],使f(x0)>g(x0)成立,则实数a的范围为( )
| 1 |
| x |
| a |
| x |
| A、[λ,+∞) |
| B、(0,+∞) |
| C、[0,+∞) |
| D、(G(x),+∞) |
函数f(x)=
的定义域为R,则实数m的取值范围是( )
| -mx2-4mx-m+3 |
| A、[-1,0] |
| B、[-1,0) |
| C、(-∞,-1]∪(0,+∞) |
| D、(-∞,-1]∪[0,+∞) |
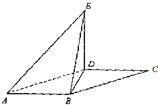 如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.
如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.