题目内容
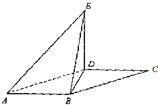 如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.
如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:由已知条件推导出∠ABD=90°,∠EDB=∠CDB=∠ABD=90°,从而得到平面EBD⊥平面ABD,由此能够证明ED⊥AB,进而结合线面垂直的判定定理得到答案.
解答:
证明:∵BD⊥AB,
∴在Rt△ABD中,BD2=AD2-AB2,
∵AB=2,AD=4,
∴BD=2
,
∴△EBD中,BD2=EB2-ED2,
∴△ABD和△EBD为直角三角形,此即ED⊥DB,
而DB又是平面EBD和平面ABD的交线,
∵平面EBD⊥平面ABD,ED?平面EBD,ED?平面ABD,DB=平面EBD∩平面ABD,
∴ED⊥平面ABD,
又∵AB?平面ABD,
∴AB⊥DE,
又∵BD⊥AB,DE∩BD=D,DE,BD?平面BDE,
∴AB⊥面BDE.
∴在Rt△ABD中,BD2=AD2-AB2,
∵AB=2,AD=4,
∴BD=2
| 3 |
∴△EBD中,BD2=EB2-ED2,
∴△ABD和△EBD为直角三角形,此即ED⊥DB,
而DB又是平面EBD和平面ABD的交线,
∵平面EBD⊥平面ABD,ED?平面EBD,ED?平面ABD,DB=平面EBD∩平面ABD,
∴ED⊥平面ABD,
又∵AB?平面ABD,
∴AB⊥DE,
又∵BD⊥AB,DE∩BD=D,DE,BD?平面BDE,
∴AB⊥面BDE.
点评:本题考查异面直线垂直的证明,考查直线与平面的判定与性质,面面垂直的性质,熟练掌握线面,线线,面面垂直之间的互相转化是解答的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
a、b为实数,则下列不等式中成立的是( )
A、a>b,则
| ||||
B、a<b,则
| ||||
C、
| ||||
D、
|
设θ∈(
,
),且17θ的终边与角θ的终边相同,则tanθ 等于( )
| π |
| 6 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
 如图,在三棱锥A-BCD中,侧面ABD与底面BCD均为等腰三角形,∠BAD=∠BCD=90°,E为BD的中点,且AE⊥CE.
如图,在三棱锥A-BCD中,侧面ABD与底面BCD均为等腰三角形,∠BAD=∠BCD=90°,E为BD的中点,且AE⊥CE.