题目内容
13．已知方程2x+x=4的解在区间（n，n+1）上，其中n∈Z，则n=1．分析 由方程与函数的关系，令f（x）=2x+x-4，从而利用零点的判定定理判断．
解答 解：令f（x）=2x+x-4，
易知f（x）=2x+x-4在R上单调递增且连续，
且f（1）=2+1-4=-1＜0，f（2）=4+2-4=2＞0，
故方程2x+x=4的解在区间（1，2）上，
故答案为：1．
点评 本题考查了方程的根与函数的零点的关系应用，关键在于构造函数f（x）=2x+x-4．
练习册系列答案
阅读快车系列答案
相关题目
3．下列说法正确的是（ ）
| A． | 命题“若a＞b，则a2＞b2”的否命题是“若a＜b，则a2＜b2” | |
| B． | 命题“若a＞b，则a2＞b2”的逆命题是“若a≤b，则a2≤b2” | |
| C． | 命题“?x∈R，cosx＜1”的否定命题是“?x0∈R，cosx0≥1” | |
| D． | 命题“?x∈R，cosx＜1”的否定命题是“?x0∈R，cosx0＞1” |
4．设函数f（x）=sinωx（ω＞0），将f（x）的图象向左平移$\frac{π}{6}$个单位长度后，所得的图象与y=cosωx的图象重合，则ω的最小值等于（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | 6 | D． | 9 |
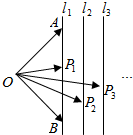如图，已知l1，l2，l3，…ln为平面内相邻两直线距离为1的一组平行线，点O到l1的距离为2，A，B是l1的上的不同两点，点P1，P2，P3，…Pn分别在直线l1，l2，l3，…ln上．若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$（n∈N*），则x1+x2+…+x5+y1+y2+…+y5的值为10．
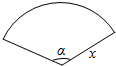如图，用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地，设扇形的半径为xm，面积为Scm2．
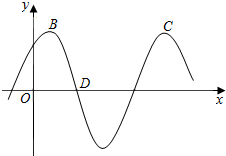如图所示，B，C两点是函数f（x）=Asin（2x+$\frac{π}{3}$）（A＞0）图象上相邻的两个最高点，D点为函数f（x）图象与x轴的一个交点．