Question

18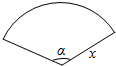．如图，用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地，设扇形的半径为xm，面积为Scm²．
（1）写出S关于x的函数表达式，并求出该函数的定义域；
（2）当半径x和圆心角α分别是多少时，所围扇形场地的面积S最大，并求S的最大值．

Answer 1

分析 （1）设扇形的弧长为l，则l=10-2x，由题意可得$\left\{\begin{array}{l}{0＜x≤3}\\{0＜10-2x＜πx}\end{array}\right.$，可得函数解析式和定义域；
（2）由（1）和基本不等式可得S=（5-x）x≤（$\frac{5-x+x}{2}$）²=$\frac{25}{4}$，由等号成立的条件可得．

解答 解：（1）设扇形的弧长为l，则l=10-2x，
由题意可得$\left\{\begin{array}{l}{0＜x≤3}\\{0＜10-2x＜πx}\end{array}\right.$，
解得$\frac{10}{π+2}$＜x≤3，
∴S=（5-x）x=-x²+5x，$\frac{10}{π+2}$＜x≤3；
（2）由（1）和基本不等式可得S=（5-x）x≤（$\frac{5-x+x}{2}$）²=$\frac{25}{4}$，
当且仅当5-x=x即x=$\frac{5}{2}$时取等号，此时l=5，圆心角α=$\frac{l}{x}$=2，
∴当半径x和圆心角α分别为$\frac{5}{2}$和2时，所围扇形场地的面积S最大，且最大值$\frac{25}{4}$

点评 本题考查三角函数的最值，涉及扇形的面积公式和基本不等式求最值，属基础题．