题目内容
3.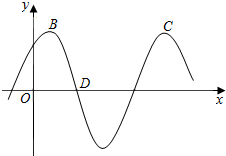 如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.
如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.(Ⅰ)若A=2,求f(x)在区间[0,$\frac{π}{2}$]上的值域;
(Ⅱ)若BD⊥CD,求A的值.
分析 (Ⅰ)由条件利用正弦函数的定义域和值域求得f(x)在区间[0,$\frac{π}{2}$]上的值域.
(Ⅱ)先由条件利用五点法作图求得BCD的坐标,再利用 $\overrightarrow{DB}•\overrightarrow{DC}$=0,求得A的值.
解答 解:(Ⅰ)若A=2,求f(x)=2sin(2x+$\frac{π}{3}$),∵x∈[0,$\frac{π}{2}$],∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴2sin(2x+$\frac{π}{3}$)∈[-$\sqrt{3}$,2].
(Ⅱ)分别令2x+$\frac{π}{3}$=$\frac{π}{2}$,2x+$\frac{π}{3}$=$\frac{5π}{2}$,求得B、C的横坐标分别为$\frac{π}{12}$,$\frac{13π}{12}$,
故B($\frac{π}{12}$,A)、C($\frac{13π}{12}$,A),可得D($\frac{π}{12}$+$\frac{1}{4}•\frac{2π}{2}$,0),即D($\frac{π}{3}$,0).
若BD⊥CD,∴$\overrightarrow{DB}•\overrightarrow{DC}$=(-$\frac{π}{4}$,A)($\frac{3π}{4}$,A)=-$\frac{3π}{16}$+A2=0,∴A=$\frac{\sqrt{3π}}{4}$.
点评 本题主要考查正弦函数的定义域和值域,两个向量垂直的性质,两个向量的数量积公式,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.已知双曲线:x2-$\frac{{y}^{2}}{4}$=1上一点P到它的一个焦点的距离为2,则它到另一个焦点的距离为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 2+2$\sqrt{5}$ |
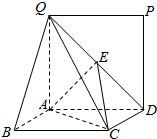 如图,矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直,E是QD的中点.
如图,矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直,E是QD的中点.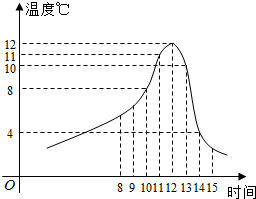 某食品的保鲜时间t(单位:小时)与储藏温度x(恒温,单位:℃)满足函数关系$t=\left\{\begin{array}{l}64,x≤0\\{2^{kx+6}},x>0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时.
某食品的保鲜时间t(单位:小时)与储藏温度x(恒温,单位:℃)满足函数关系$t=\left\{\begin{array}{l}64,x≤0\\{2^{kx+6}},x>0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时.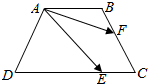 如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.
如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.