题目内容
5.已知直线l经过直线2x+y-5=0与x-2y=0的交点P.(Ⅰ)若直线l平行于直线l1:4x-y+1=0,求l的方程;
(Ⅱ)若直线l垂直于直线l1:4x-y+1=0,求l的方程.
分析 联立$\left\{\begin{array}{l}{2x+y-5=0}\\{x-2y=0}\end{array}\right.$,解得交点P.
(Ⅰ)设直线l:4x-y+m=0,把(2,1)代入可得m,即可得出;
(Ⅱ)设直线l的方程为:x+4y+n=0,把点P(2,1)代入上述方程n,即可得出.
解答 解:联立$\left\{\begin{array}{l}{2x+y-5=0}\\{x-2y=0}\end{array}\right.$,解得P(2,1).
(Ⅰ)设直线l:4x-y+m=0,把(2,1)代入可得:4×2-1+m=0,m=-7.
∴l的方程为:4x-y-7=0;
(Ⅱ)设直线l的方程为:x+4y+n=0,
把点P(2,1)代入上述方程可得:2+4+n=0,解得n=-6.
∴x+4y-6=0.
点评 本题考查了相互垂直的直线、相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0,一个焦点与抛物线y2=-20x的焦点重合,则双曲线的方程为( )( )
| A. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | ||
| C. | $\frac{3{x}^{2}}{25}$-$\frac{3{y}^{2}}{100}$=1 | D. | $\frac{3{x}^{2}}{100}$-$\frac{3{y}^{2}}{25}$=1 |
20.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程为$y=\frac{3}{4}x$,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |
10.抛物线y2=8x上横坐标为1的点到其焦点F距离为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |

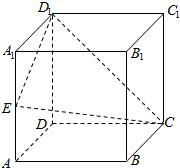 如图,有一个正方体的木块,E为棱AA1的中点.现因实际需要,需要将其沿平面D1EC将木块锯开.请你画出前面ABB1A1与截面D1EC的交线,并说明理由.
如图,有一个正方体的木块,E为棱AA1的中点.现因实际需要,需要将其沿平面D1EC将木块锯开.请你画出前面ABB1A1与截面D1EC的交线,并说明理由.