题目内容
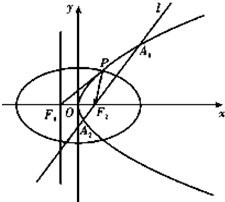 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,且C1的焦 点为F2;以F1,F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,且C1的焦 点为F2;以F1,F2为焦点,离心率e=| 1 |
| 2 |
(Ⅰ)是否存在实数m,使得△PF1F2的边长是连续的自然数,若存在,求出这样的实数m,若不存在,请说明理由;
(Ⅱ)若m=1,直线l经过椭圆C2的右焦点F2,且与抛物线C1交于A1,A2,以线段A1A2为直径作圆,若圆经过点P,求直线l的斜率.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)假设存在实数m,在△PF1F2中,|PF1|最长,|PF2|最短,令|F1F2|=2c=2m,则|PF1|=2m+1,|PF2|=2m-1,把P(m-1,4m(m-1))代入椭圆方程求出m值.
(Ⅱ)依题意设直线l的方程为:x=ky+1,k∈R,代入椭圆方程,可得点P的坐标为P(
,
),将x=ky+1代入y2=4x得y2-4ky-4=0,由圆经过点P,可得
•
=0,即可求出直线l的斜率.
(Ⅱ)依题意设直线l的方程为:x=ky+1,k∈R,代入椭圆方程,可得点P的坐标为P(
| 2 |
| 3 |
2
| ||
| 3 |
| PA1 |
| PA2 |
解答:
解:(Ⅰ)∵C1:y2=4mx(m>0)的右焦点F2(m,0)
∴椭圆的半焦距c=m,
又e=
,
∴椭圆的长半轴的长a=2m,短半轴的长b=
m,
∴椭圆方程为
+
=1.
假设存在实数m,△PF1F2中的边长是连续自然数,则在△PF1F2中,|PF1|最长,|PF2|最短,
令|F1F2|=2c=2m,则|PF1|=2m+1,|PF2|=2m-1.
由抛物线的定义可得|PF2|=2m-1=xP-(-m),∴xP=m-1.
把P(m-1,4m(m-1))代入椭圆
+
=1,解得m=3.
故存在实数m=3满足条件.
(Ⅱ)依题意设直线l的方程为:x=ky+1,k∈R
代入椭圆方程,可得点P的坐标为P(
,
).
将x=ky+1代入y2=4x得y2-4ky-4=0.
设A1(x1,y1)、A2(x2,y2),由韦达定理得y1+y2=4k,y1y2=-4.
∵圆经过点P,
∴
•
=0,
∴(x1-
,y1-
)•(x2-
,y2-
)=0,
∴-
=0,
∴k=
或
.
∴椭圆的半焦距c=m,
又e=
| 1 |
| 2 |
∴椭圆的长半轴的长a=2m,短半轴的长b=
| 3 |
∴椭圆方程为
| x2 |
| 4m2 |
| y2 |
| 3m2 |
假设存在实数m,△PF1F2中的边长是连续自然数,则在△PF1F2中,|PF1|最长,|PF2|最短,
令|F1F2|=2c=2m,则|PF1|=2m+1,|PF2|=2m-1.
由抛物线的定义可得|PF2|=2m-1=xP-(-m),∴xP=m-1.
把P(m-1,4m(m-1))代入椭圆
| x2 |
| 4m2 |
| y2 |
| 3m2 |
故存在实数m=3满足条件.
(Ⅱ)依题意设直线l的方程为:x=ky+1,k∈R
代入椭圆方程,可得点P的坐标为P(
| 2 |
| 3 |
2
| ||
| 3 |
将x=ky+1代入y2=4x得y2-4ky-4=0.
设A1(x1,y1)、A2(x2,y2),由韦达定理得y1+y2=4k,y1y2=-4.
∵圆经过点P,
∴
| PA1 |
| PA2 |
∴(x1-
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
∴-
24k2+24
| ||
| 9 |
∴k=
| ||
| 12 |
11
| ||
| 12 |
点评:本题考查抛物线和椭圆的标准方程和简单性质,考查直线与椭圆的位置关系,同时考查向量知识的运用,综合性较强,属于中档题.

练习册系列答案
相关题目
在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字的和是奇数的概率是( )
| A、0.3 | B、0.4 |
| C、0.5 | D、0.6 |
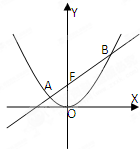 抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点
抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点