题目内容
已知函数f(x)=x2+x+b(b为实数)与x轴交于A、B两点,与y轴交于点C(C点异于A、B).
(1)求b的取值范围;
(2)求过三点A、B、C的圆的方程.
(1)求b的取值范围;
(2)求过三点A、B、C的圆的方程.
考点:圆的标准方程,二次函数的性质
专题:直线与圆
分析:(1)直接一判别式大于0,即可求b的取值范围;
(2)求出三点A、B、C的坐标,设出圆的圆心坐标,求出圆心坐标以及半径,即可得到圆的方程
(2)求出三点A、B、C的坐标,设出圆的圆心坐标,求出圆心坐标以及半径,即可得到圆的方程
解答:
解:(1)函数 y=x2+x+b 的图象,与x轴交于A、B两点,则△=1-4b>0,得 b<
.
函数 y=x2+x+b 的图象,与y轴交于点C(C点异于A、B),
得 b≠0.则 0≠b<
.
(2)y=x2+x+b=(x+
)2+b-
,
三点坐标:A(
,0),B(
,0),C(0,b).
过三点A、B、C的圆的圆心G在直线 x=-
上,设G(-
,y),
则GA=GC,得 y2+
=
+(y-b)2,则 y=
,
半径 r=
.
则圆方程为 (x+
)2+(y-
)2=
.
| 1 |
| 4 |
函数 y=x2+x+b 的图象,与y轴交于点C(C点异于A、B),
得 b≠0.则 0≠b<
| 1 |
| 4 |
(2)y=x2+x+b=(x+
| 1 |
| 2 |
| 1 |
| 4 |
三点坐标:A(
-1-
| ||
| 2 |
-1+
| ||
| 2 |
过三点A、B、C的圆的圆心G在直线 x=-
| 1 |
| 2 |
| 1 |
| 2 |
则GA=GC,得 y2+
| 1-4b |
| 4 |
| 1 |
| 4 |
| 1+b |
| 2 |
半径 r=
| ||
| 2 |
则圆方程为 (x+
| 1 |
| 2 |
| b+1 |
| 2 |
| (b-1)2+1 |
| 4 |
点评:本题看圆的方程的求法,二次函数的基本性质,考查基本知识的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
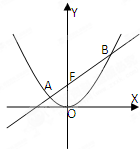 抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点
抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点 若F1、F2分别是椭圆
若F1、F2分别是椭圆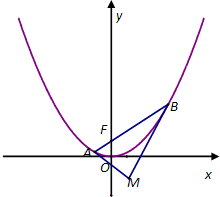 如图示:已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点,经过A、B两点分别作抛物线C的切线l1、l2,切线l1与l2相交于点M.
如图示:已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点,经过A、B两点分别作抛物线C的切线l1、l2,切线l1与l2相交于点M.