题目内容
已知函数y=f（x）在（0，+∞）上为减函数，且f（x）＜0（x＞0），试判断f（x）=
在（0，+∞）上的单调性，并给出证明过程．
| 1 |
| f(x) |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：首先，设x1，x2∈（0，+∞），且x1＜x2，然后，比较大小，从而得到结论．
解答：
解：函数g(x)=
为（0，+∞）上增函数，证明如下：
任设x1，x2∈（0，+∞）且x1＜x2，
∵y=f（x）在（0，+∞）上为减函数，
∴f（x1）＞f（x2），f（x1）＜0，f（x2）＜0，
g(x1)-g(x2)=
-
=
，
∵f（x1）＞f（x2），
∴f（x2）-f（x1）＜0，
∵f（x1）＜0，f（x2）＜0，
∴f（x1）•f（x2）＞0，
∴g（x1）-g（x2）＜0，
∴g(x)=
为（0，+∞）上的增函数．
| 1 |
| f(x) |
任设x1，x2∈（0，+∞）且x1＜x2，
∵y=f（x）在（0，+∞）上为减函数，
∴f（x1）＞f（x2），f（x1）＜0，f（x2）＜0，
g(x1)-g(x2)=
| 1 |
| f(x1) |
| 1 |
| f(x2) |
=
| f(x2)-f(x1) |
| f(x1)f(x2) |
∵f（x1）＞f（x2），
∴f（x2）-f（x1）＜0，
∵f（x1）＜0，f（x2）＜0，
∴f（x1）•f（x2）＞0，
∴g（x1）-g（x2）＜0，
∴g(x)=
| 1 |
| f(x) |
点评：本题重点考查函数的单调性的应用，属于中档题，难度中等．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
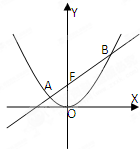抛物线C：x2=2py（p＞0）的焦点为F，O为坐标原点；当抛物线上点N的纵坐标为1时，|NF|=2，已知直线l经过抛物线C的焦点F，且与抛物线C交于A，B两点
若F1、F2分别是椭圆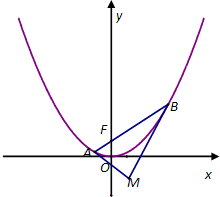
如图示：已知抛物线C：x2=4y的焦点为F，过点F作直线l交抛物线C于A、B两点，经过A、B两点分别作抛物线C的切线l1、l2，切线l1与l2相交于点M．