题目内容
已知动圆过定点A(0,2),且在x轴上截得的弦MN的长为4.
(1)求动圆圆心的轨迹C的方程;
(2)过点A(0,2)作一条直线与曲线C交于E,F两点,过E,F分别作曲线C的切线,两切线交于P点,当|PE|•|PF|最小时,求直线EF的方程.
(1)求动圆圆心的轨迹C的方程;
(2)过点A(0,2)作一条直线与曲线C交于E,F两点,过E,F分别作曲线C的切线,两切线交于P点,当|PE|•|PF|最小时,求直线EF的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设圆心为C(x,y),线段MN的中点为E,依题意得|CA|2=|CM|2=|ME|2+|EC|2,由此能求出动圆圆心的轨迹C的方程.
(2)设E(x1,
),F(x2,
),由A,E,F三点共线,得到x1x2=-8,由已知条件利用导数性质求出P点坐标为(
,-2),由此能求出|PE|•|OF|当且仅当x2=-x1时取最小值,从而能求出直线EF方程为y=2.
(2)设E(x1,
| x12 |
| 4 |
| x22 |
| 4 |
| x1+x2 |
| 2 |
解答:
解:(1)设圆心为C(x,y),线段MN的中点为E,则|ME|=
,
依题意得|CA|2=|CM|2=|ME|2+|EC|2,
∴x2+(y-2)2=22+y2,整理,得x2=4y,
∴动圆圆心的轨迹C的方程为x2=4y.
(2)设E(x1,
),F(x2,
),
由A,E,F三点共线,得
=
,∴x1x2=-8,
由x2=4y,得y=
x2,∴y′=
x,
∴PE的方程为y=
=
(x-x1),即y=
x-
x12.
同理PF的方程为y=
x-
x22,
解得P点坐标为(
,
),即(
,-2),
∴|PE|=
•|
-x1|=
,
∴|PE|•|OF|=
=
=
=
≥
=24,
当且仅当x2=-x1时,上式取等号,
此时EF的斜率为0,所求直线EF方程为y=2.
| |MN| |
| 2 |
依题意得|CA|2=|CM|2=|ME|2+|EC|2,
∴x2+(y-2)2=22+y2,整理,得x2=4y,
∴动圆圆心的轨迹C的方程为x2=4y.
(2)设E(x1,
| x12 |
| 4 |
| x22 |
| 4 |
由A,E,F三点共线,得
| ||
| x2 |
| ||
| x1 |
由x2=4y,得y=
| 1 |
| 4 |
| 1 |
| 2 |
∴PE的方程为y=
| x12 |
| 4 |
| x1 |
| 2 |
| x1 |
| 2 |
| 1 |
| 4 |
同理PF的方程为y=
| x2 |
| 2 |
| 1 |
| 4 |
解得P点坐标为(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
| x1+x2 |
| 2 |
∴|PE|=
1+
|
| x1+x2 |
| 2 |
(x2-x1)•
| ||
| 4 |
∴|PE|•|OF|=
(x2-x1)2•
| ||
| 16 |
=
(x12+x22+16)•
| ||
| 16 |
=
(x12+x22+16)•
| ||
| 16 |
=
(x12+x22+16)•
| ||
| 8 |
≥
(2|x1x2|+16)•
| ||
| 8 |
当且仅当x2=-x1时,上式取等号,
此时EF的斜率为0,所求直线EF方程为y=2.
点评:本题考查动圆圆心的轨迹方程的求法,考查考查直线方程的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
下列说法正确的是( )
| A、若已知两个变量具有线性相关关系,且它们正相关,则其线性回归直线的斜率为正 |
| B、直线l垂直于平面α的充要条件为l垂直于平面α内的无数条直线 |
| C、若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,则P(ξ>10.1)=0.3174 |
| D、已知命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2<0 |
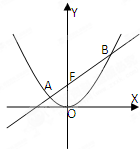 抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点
抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点