题目内容
已知函数f(x)=kx+lnx(k是常数).
(1)讨论函数f(x)的单调性;
(2)当k=0时,是否存在不相等的正数a,b满足
=f′(
)?若存在,求出a,b;若不存在,说明理由.
(1)讨论函数f(x)的单调性;
(2)当k=0时,是否存在不相等的正数a,b满足
| f(a)-f(b) |
| a-b |
| a+b |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导f′(x)=
,(x>0),从而讨论导数的正负以确定函数的单调性;
(2)不妨设存在a>b>0合题意,从而可得ln
=
;令
=x得lnx=
;构造函数F(x)=lnx-
,(x≥1);从而转化为函数的最值问题.
| kx+1 |
| x |
(2)不妨设存在a>b>0合题意,从而可得ln
| a |
| b |
| 2(a-b) |
| a+b |
| a |
| b |
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
解答:
解:(1)f′(x)=
,(x>0)
①当k≥0时,f′(x)>0;
故函数f(x)在定义域上单调递增;
②当k<0时,当x∈(0,-
)时,f′(x)>0;
当x∈(-
,+∞)时,f′(x)<0;
故函数f(x)在(0,-
)上单调递增,在(-
,+∞)上单调递减;
(2)不妨设存在a>b>0合题意,
则整理可得,ln
=
;
令
=x得,lnx=
;
则构造函数F(x)=lnx-
,(x≥1);
则F(1)=0,F′(x)=
≥0;
故F(x)在[1,+∞)上单调递增,
故F(
)>F(1)=0;
故与ln
=
相矛盾;
故假设不成立,
即符合题意的不相等的正数a,b不存在.
| kx+1 |
| x |
①当k≥0时,f′(x)>0;
故函数f(x)在定义域上单调递增;
②当k<0时,当x∈(0,-
| 1 |
| k |
当x∈(-
| 1 |
| k |
故函数f(x)在(0,-
| 1 |
| k |
| 1 |
| k |
(2)不妨设存在a>b>0合题意,
则整理可得,ln
| a |
| b |
| 2(a-b) |
| a+b |
令
| a |
| b |
| 2(x-1) |
| x+1 |
则构造函数F(x)=lnx-
| 2(x-1) |
| x+1 |
则F(1)=0,F′(x)=
| (x-1)2 |
| x(x+1)2 |
故F(x)在[1,+∞)上单调递增,
故F(
| a |
| b |
故与ln
| a |
| b |
| 2(a-b) |
| a+b |
故假设不成立,
即符合题意的不相等的正数a,b不存在.
点评:本题考查了导数的综合应用及存在性命题的判断,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知等比数列{an}的公比为q,且a1>0,则“q>0”是“数列{an}为递增数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知实数x,y满足
则z=2x-y的最小值是( )
|
| A、5 | ||
B、
| ||
| C、-5 | ||
D、-
|
 直三棱柱ABC-A1B1C1中,CB1⊥BA1,∠CAB=
直三棱柱ABC-A1B1C1中,CB1⊥BA1,∠CAB=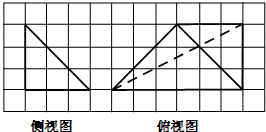 如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )
如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )