题目内容
 已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.
已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.(Ⅰ)若第五组抽出的号码为22,写出所有被抽出职工的号码;
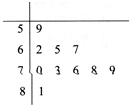
(Ⅱ)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的平均数;
(Ⅲ)在(Ⅱ)的条件下,从体重不轻于73公斤(≥73公斤)的职工中随机抽取两名职工,求被抽到的两名职工的体重之和等于154公斤的概率.
考点:列举法计算基本事件数及事件发生的概率,茎叶图
专题:概率与统计
分析:(Ⅰ)根据各组内抽取的编号依次增加5进行系统抽样,可得抽出的10名职工的号码,
(Ⅱ)计算10名职工的平均体重,
(Ⅲ)写出从10名职工中随机抽取两名体重不轻于73公斤的职工的取法,从而可求被抽到的两名职工的体重之和等于154公斤的概率..
(Ⅱ)计算10名职工的平均体重,
(Ⅲ)写出从10名职工中随机抽取两名体重不轻于73公斤的职工的取法,从而可求被抽到的两名职工的体重之和等于154公斤的概率..
解答:
解:( I)由题意,第5组抽出的号码为22.
因为2+5×(5-1)=22,所以第1组抽出的号码应该为2,抽出的10名职工的号码依次分别为:2,7,12,17,22,27,32,37,42,47.
( II)这10名职工的平均体重为:
=
×(81+70+73+76+78+79+62+65+67+59)=71,
( III)从这10名职工中随机抽取两名体重不轻于73公斤的职工,共有10种不同的取法:(73,76),(73,78),(73,79),(73,81),(76,78),(76,79),(76,81),(78,79),(78,81),(79,81),
其中体重之和大于等于154公斤的有7种.故所求概率P=
.
因为2+5×(5-1)=22,所以第1组抽出的号码应该为2,抽出的10名职工的号码依次分别为:2,7,12,17,22,27,32,37,42,47.
( II)这10名职工的平均体重为:
. |
| x |
| 1 |
| 10 |
( III)从这10名职工中随机抽取两名体重不轻于73公斤的职工,共有10种不同的取法:(73,76),(73,78),(73,79),(73,81),(76,78),(76,79),(76,81),(78,79),(78,81),(79,81),
其中体重之和大于等于154公斤的有7种.故所求概率P=
| 7 |
| 10 |
点评:本题考查系统抽样,考查样本方差,考查列举法求基本事件,属于基础题.

练习册系列答案
相关题目
设S={x||x|<3},T={x|3x-5<1},则S∩T=( )
| A、∅ |
| B、{x|-3<x<3} |
| C、{x|-3<x<2} |
| D、{x|2<x<3} |
a,b是异面直线,点P∉a∪b,下列命题:
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
已知定义域为R的函数f (x)满足对任意的x1,x2∈(8,+∞)(x1<x2),有f(x1)>f(x2),且函数y=f(x+8)为偶函数,则( )
| A、f (6)>f (7) |
| B、f (6)>f (9) |
| C、f (7)>f (9) |
| D、f (7)>f (10) |
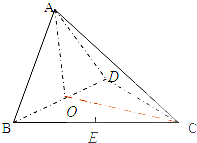 如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=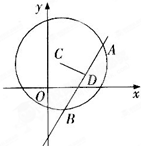 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.