题目内容
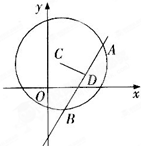 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.(1)求证:无论m为何值,直线l恒过定点(3,1);
(2)当m为何值时,直线被圆截得的弦最短,最短的弦长是多少?
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(1)通过直线l转化为直线系,求出直线恒过的定点;
(2)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出m的值,再由勾股定理即可得到最短弦长.
(2)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出m的值,再由勾股定理即可得到最短弦长.
解答:
(1)证明:将l的方程整理为(x+y-4)+m(2x+y-7)=0,
由
,解得
,
则无论m为何值,直线l过定点D(3,1).
(2)解:因为(3-1)2+(1-2)2=5<25,
则点D在圆C的内部,直线l与圆C相交.
圆心C(1,2),半径为5,|CD|=
=
,
当截得的弦长最小时,l⊥CD,由于kCD=
=-
,
则l的斜率为2,即有-
=2,解得m=-
.
此时最短弦长为2
=4
,
故当m=-
时,直线被圆截得的弦最短,最短的弦长是4
.
由
|
|
则无论m为何值,直线l过定点D(3,1).
(2)解:因为(3-1)2+(1-2)2=5<25,
则点D在圆C的内部,直线l与圆C相交.
圆心C(1,2),半径为5,|CD|=
| (3-1)2+(1-2)2 |
| 5 |
当截得的弦长最小时,l⊥CD,由于kCD=
| 2-1 |
| 1-3 |
| 1 |
| 2 |
则l的斜率为2,即有-
| 2m+1 |
| m+1 |
| 3 |
| 4 |
此时最短弦长为2
| 52-5 |
| 5 |
故当m=-
| 3 |
| 4 |
| 5 |
点评:本题考查直线系方程的应用,考查直线与圆的位置关系,考查平面几何知识的运用,考查计算能力,属于中档题.

练习册系列答案
相关题目
椭圆
+
=1(a>b>0)的两个焦点是F1、F2,以|F1F2|为斜边作等腰直角三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
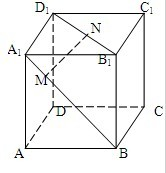 如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.
如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.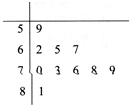 已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.
已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.