题目内容
已知f(x)=cos2x+4sinx.
(Ⅰ)求f′(-
)的值;
(Ⅱ)求f(x)的最大值以及取得最大值时x的值.
(Ⅰ)求f′(-
| π |
| 4 |
(Ⅱ)求f(x)的最大值以及取得最大值时x的值.
考点:正弦函数的单调性,导数的运算
专题:三角函数的图像与性质
分析:(Ⅰ)求函数的导数,即可求f′(-
)的值;
(Ⅱ)利用三角函数的图象和性质,即可求f(x)的最大值以及取得最大值时x的值.
| π |
| 4 |
(Ⅱ)利用三角函数的图象和性质,即可求f(x)的最大值以及取得最大值时x的值.
解答:
解:(Ⅰ)f′(x)=-2sin2x+4cosx,
则f′(-
)=-2sin(-
)+4cos(-
)=2+4×
=2+2
;
(Ⅱ)f(x)=1-2sin2x+4sinx=-2(sinx-1)2+3,
因为sinx∈[-1,1],所以当sinx=1即x=
+2kπ,k∈Z时,f(x)取最大值3.
则f′(-
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| ||
| 2 |
| 2 |
(Ⅱ)f(x)=1-2sin2x+4sinx=-2(sinx-1)2+3,
因为sinx∈[-1,1],所以当sinx=1即x=
| π |
| 2 |
点评:本题主要考查三角函数的单调性的应用,利用三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
已知直线l1:x+ky-2k=0与l2:kx-(k-2)y+1=0垂直,则k的值是( )
| A、1 | B、3 | C、1或-2 | D、0或3 |
设P是不等式组
表示的平面区域内的任意一点,向量
=(1,1),
=(2,1),若
=λ
+μ
(λ,μ为实数),则λ-μ的最大值为( )
|
| m |
| n |
| OP |
| m |
| n |
| A、4 | B、3 | C、-1 | D、-2 |
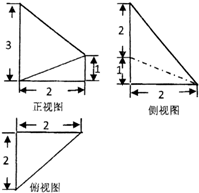
已知某几何体的三视图如图所示,则该几何体的体积为( )

| A、8 | ||
B、
| ||
| C、4 | ||
| D、12 |
 学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?
学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?