题目内容
QQ先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).
(1)求这7条鱼中至少有5条被QQ先生吃掉的概率;
(2)以ξ表示这7条鱼中被QQ先生吃掉的鱼的条数,求Eξ.
(1)求这7条鱼中至少有5条被QQ先生吃掉的概率;
(2)以ξ表示这7条鱼中被QQ先生吃掉的鱼的条数,求Eξ.
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:应用题,概率与统计
分析:(1)确定最坏的情况的概率,利用对立事件的概率公式,可求这7条鱼中至少有5条被QQ先生吃掉的概率;
(2)QQ先生能吃到的鱼的条数ξ可取4,5,6,7,求出相应的概率,可得ξ的分布列和数学期望.
(2)QQ先生能吃到的鱼的条数ξ可取4,5,6,7,求出相应的概率,可得ξ的分布列和数学期望.
解答:
解:(1)QQ先生能吃到的鱼的条数ξ可取4,5,6,7,最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉,第4天QQ先生吃掉黑鱼,其概率为P(ξ=4)=
×
×
=
故QQ先生至少吃掉5条鱼的概率是P(ξ≥5)=1-P(ξ=4)=
.
(2)与(1)相仿地可得,(6分)
P(ξ=5)=
×
×
=
,P(ξ=6)=
×
=
,P(ξ=7)=
=
故Eξ=
+
+
+
=5,
故所求期望值为5.(12分)
| 6 |
| 7 |
| 4 |
| 5 |
| 2 |
| 3 |
| 16 |
| 35 |
故QQ先生至少吃掉5条鱼的概率是P(ξ≥5)=1-P(ξ=4)=
| 19 |
| 35 |
(2)与(1)相仿地可得,(6分)
P(ξ=5)=
| 6 |
| 7 |
| 4 |
| 5 |
| 1 |
| 3 |
| 8 |
| 35 |
| 6 |
| 7 |
| 1 |
| 5 |
| 6 |
| 35 |
| 1 |
| 7 |
| 5 |
| 35 |
故Eξ=
| 4×16 |
| 35 |
| 5×8 |
| 35 |
| 6×6 |
| 35 |
| 7×5 |
| 35 |
故所求期望值为5.(12分)
点评:本题考查概率知识,考查离散型随机变量的分布列与数学期望,确定变量的取值,正确求概率是关键.

练习册系列答案
相关题目
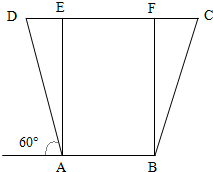 如图,水渠的横截面积是等腰梯形,下底及两边坡的总长度为a,坡AD的倾角为60°,
如图,水渠的横截面积是等腰梯形,下底及两边坡的总长度为a,坡AD的倾角为60°,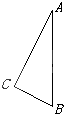 已知直角三角形ABC的斜边长AB=2,现以斜边AB为轴旋转一周,得旋转体.
已知直角三角形ABC的斜边长AB=2,现以斜边AB为轴旋转一周,得旋转体.