题目内容
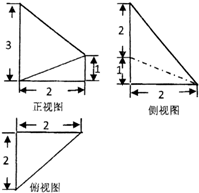
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、8 | ||
B、
| ||
| C、4 | ||
| D、12 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何体是一个以主视图为底面的棱锥，分别求出底面面积和棱锥的高，进而可得几何体的体积．
解答：
解：由已知中的三视图可得，该几何是一个以主视图为底面的棱锥，
∵底面是一个上下底边长为1和3，高为2的梯形，
故底面面积S底=
×(1+3)×2=4，
棱锥的高h=2，
故棱锥的体积V=
S底h=
×4×2=
，
故选：B
∵底面是一个上下底边长为1和3，高为2的梯形，
故底面面积S底=
| 1 |
| 2 |
棱锥的高h=2，
故棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
故选：B
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
设f（x）=2x+x-4，则函数f（x）的零点位于区间（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
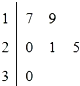某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则恰有1名优秀工人的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知a，b＞0，实数x，y满足不等式组
，则当
+
取得最小值时，z=bx+ay取最大值的最优解为（ ）
|
| 2a |
| a+b |
| b |
| a |
| A、（0，0） | ||||
| B、（1，0） | ||||
| C、（0，1） | ||||
D、（
|
不等式组
所表示的平面区域的面积等于6，则a的值为（ ）
|
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
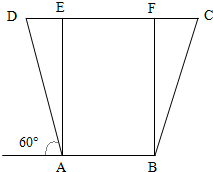如图，水渠的横截面积是等腰梯形，下底及两边坡的总长度为a，坡AD的倾角为60°，