题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2
cosB-sin(A-B)sinB+cos(A+C)=-
(Ⅰ)求角A;
(Ⅱ)若a=5
,b=5,求角B及△ABC的面积.
| A-B |
| 2 |
| 1 |
| 2 |
(Ⅰ)求角A;
(Ⅱ)若a=5
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:解三角形
分析:(Ⅰ)利用二倍角公式和两角和公式对原式化简整理求得cosA的值.
(Ⅱ)利用正弦定理求得sinB的值,进而求得B,利用三角形内角和求得C,最后利用三角形面积公式求得其面积.
(Ⅱ)利用正弦定理求得sinB的值,进而求得B,利用三角形内角和求得C,最后利用三角形面积公式求得其面积.
解答:
解:( I)∵2cos2
cosB-sin(A-B)sinB+cos(A+C)=-
,
∴[cos(A-B)+1]cosB-sin(A-B)sinB-cosB=-
∴cos(A-B+B)=-
,即cosA=-
,
∴A=
;
(Ⅱ)∵sinA=
,由正弦定理,
=
,
∴sinB=
,
∵a>b,
∴A>B,
∴B=
,
∴C=π-A-B=
,
∴S=
×5×5
×sinC=
.
综上所述,B=
;△ABC的面积为
.
| A-B |
| 2 |
| 1 |
| 2 |
∴[cos(A-B)+1]cosB-sin(A-B)sinB-cosB=-
| 1 |
| 2 |
∴cos(A-B+B)=-
| 1 |
| 2 |
| 1 |
| 2 |
∴A=
| 2π |
| 3 |
(Ⅱ)∵sinA=
| ||
| 2 |
| a |
| sinA |
| b |
| sinB |
∴sinB=
| 1 |
| 2 |
∵a>b,
∴A>B,
∴B=
| π |
| 6 |
∴C=π-A-B=
| π |
| 6 |
∴S=
| 1 |
| 2 |
| 3 |
| 25 |
| 4 |
| 3 |
综上所述,B=
| π |
| 6 |
| 25 |
| 4 |
| 3 |
点评:本题主要考查了正弦定理、余弦定理的应用,三角形恒等变换的应用.考查了对三角函数基础知识的综合运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
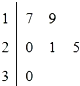 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为( )
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则恰有1名优秀工人的概率为( )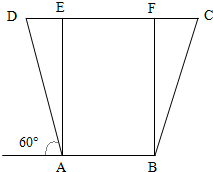 如图,水渠的横截面积是等腰梯形,下底及两边坡的总长度为a,坡AD的倾角为60°,
如图,水渠的横截面积是等腰梯形,下底及两边坡的总长度为a,坡AD的倾角为60°,