题目内容
设P是不等式组
表示的平面区域内的任意一点，向量
=（1，1），
=（2，1），若
=λ
+μ
（λ，μ为实数），则λ-μ的最大值为（ ）
|
| m |
| n |
| OP |
| m |
| n |
| A、4 | B、3 | C、-1 | D、-2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：根据向量线性运算的坐标公式，得到
，由此代入题中的不等式组，可得关于λ、μ的不等式组．作出不等式组表示的平面区域，利用数形结合即可得到结论．
|
解答：
解：∵向量
=（1，1），
=（2，1），若
=λ
+μ
（λ，μ∈R），
∴P（x，y）满足
，代入不等式组组
，
得
，
设λ=x，μ=y，则不等式等价为
，
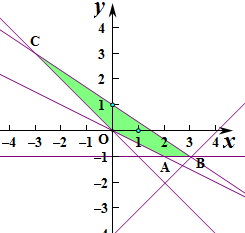
作出不等式组表示的平面区域（阴影部分），
设z=λ-μ=x-y，
即y=x-z，平移直线y=x-z，
则当直线y=x-z经过点B时，直线的截距最小，此时z最大，
由
，解得
，即B（3，-1），
此时z=x-y=3-（-1）=3+1=4，
即λ-μ的最大值为4，
故选：A．
解：∵向量| m |
| n |
| OP |
| m |
| n |
∴P（x，y）满足
|
|
得
|
设λ=x，μ=y，则不等式等价为
|
作出不等式组表示的平面区域（阴影部分），
设z=λ-μ=x-y，
即y=x-z，平移直线y=x-z，
则当直线y=x-z经过点B时，直线的截距最小，此时z最大，
由
|
|
此时z=x-y=3-（-1）=3+1=4，
即λ-μ的最大值为4，
故选：A．
点评：本题主要考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，将条件转换为关于λ、μ的不等式组是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
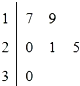某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则恰有1名优秀工人的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
设集合U={1，2，3，4，5}，M={l，3，5}，则∁UM=（ ）
| A、{1，2，4} |
| B、{1，3，5} |
| C、{2，4} |
| D、U |
已知a，b＞0，实数x，y满足不等式组
，则当
+
取得最小值时，z=bx+ay取最大值的最优解为（ ）
|
| 2a |
| a+b |
| b |
| a |
| A、（0，0） | ||||
| B、（1，0） | ||||
| C、（0，1） | ||||
D、（
|
不等式组
所表示的平面区域的面积等于6，则a的值为（ ）
|
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |