题目内容
已知直线l1：x+ky-2k=0与l2：kx-（k-2）y+1=0垂直，则k的值是（ ）
| A、1 | B、3 | C、1或-2 | D、0或3 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：由已知条件推导出k+[-（k-2）]•k=0，由此能求出k的值．
解答：
解：∵直线l1：x+ky-2k=0与l2：kx-（k-2）y+1=0垂直，
∴k+[-（k-2）]•k=0，
解得k=0或k=3．
故选：D．
∴k+[-（k-2）]•k=0，
解得k=0或k=3．
故选：D．
点评：本题考查k的值的求法，解题时要认真审题，注意直线垂直的条件的合理运用．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
设f（x）=2x+x-4，则函数f（x）的零点位于区间（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
若函数f（x）=2cos2ωx的最小正周期为π，则f（
）的值等于（ ）
| π |
| 4 |
| A、2 | ||||
B、1+
| ||||
| C、1 | ||||
| D、0 |
阅读程序框图，运行相应的程序，若输入n的值为1，则输出的S的值为（ ）
| A、176 | B、160 |
| C、145 | D、117 |
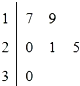某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则恰有1名优秀工人的概率为（ ）