题目内容
在△ABC中,角A,B,C的对边分别是a,b,c,且acosB-bcosA=
c.
(Ⅰ)求证tanA=3tanB;
(Ⅱ)若B=45°,b=
,求△ABC的面积.
| 1 |
| 2 |
(Ⅰ)求证tanA=3tanB;
(Ⅱ)若B=45°,b=
| 5 |
考点:正弦定理,同角三角函数基本关系的运用
专题:解三角形
分析:(Ⅰ)题中等式利用正弦定理化简,利用同角三角函数间基本关系整理即可得证;
(Ⅱ)由tanB的值确定出tanA的值,进而求出sinA与cosA的值,由sinC=sin(A+B),利用两角和与差的正弦函数公式化简,将各自的值代入求出sinC的值,利用正弦定理求出c的值,由b,c,sinA的值,利用三角形面积公式即可求出三角形ABC面积.
(Ⅱ)由tanB的值确定出tanA的值,进而求出sinA与cosA的值,由sinC=sin(A+B),利用两角和与差的正弦函数公式化简,将各自的值代入求出sinC的值,利用正弦定理求出c的值,由b,c,sinA的值,利用三角形面积公式即可求出三角形ABC面积.
解答:
解:(Ⅰ)∵acosB-bcosA=
c,
∴由正弦定理化简得:sinAcosB-sinBcosA=
sinC=
sin(A+B)=
sinAcosB+
cosAsinB,
整理得:sinAcosB=3cosAsinB,
∵cosAcosB≠0,
∴tanA=3tanB;
(Ⅱ)∵tanA=3,∴sinA=
,cosA=
,
由正弦定理
=
得:a=
=
=3,
∵sinC=sin(A+B)=sinAcosB+cosAsinB=
×
+
×
=
,
∴S△ABC=
absinC=
×3×
×
=3.
| 1 |
| 2 |
∴由正弦定理化简得:sinAcosB-sinBcosA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得:sinAcosB=3cosAsinB,
∵cosAcosB≠0,
∴tanA=3tanB;
(Ⅱ)∵tanA=3,∴sinA=
3
| ||
| 10 |
| ||
| 10 |
由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
| ||||||
|
∵sinC=sin(A+B)=sinAcosB+cosAsinB=
3
| ||
| 10 |
| ||
| 2 |
| ||
| 10 |
| ||
| 2 |
2
| ||
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
2
| ||
| 5 |
点评:此题考查了正弦定理,同角三角函数间的基本关系,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
已知p:
≥1,q:a-1<x<a+1,若p是q的充分不必要条件,则实数a的取值范围为( )
| 1 |
| x-2 |
| A、(-∞,3] |
| B、[2,3] |
| C、(2,3] |
| D、(2,3) |
已知集合A={x|x2+2x-3<0},B={x|-
<x<1},则A∩B=( )
| 2 |
| A、∅ | ||
| B、{x|-3<x<1} | ||
C、{x|-
| ||
| D、A |
已知抛物线C:y2=2x上一点P到y轴的距离为3,则 P到焦点的距离为( )
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
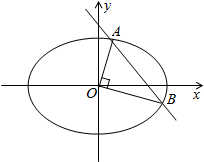 已知焦点在x轴上的椭圆
已知焦点在x轴上的椭圆