题目内容
已知曲线C1:
(t为参数,C2:
(θ为参数).
(Ⅰ)C1、C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数t=
,Q为C2上的动点,求PQ中点M到直线C3:
(t为参数)距离的最小值.
|
|
(Ⅰ)C1、C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数t=
| π |
| 2 |
|
考点:圆的参数方程
专题:坐标系和参数方程
分析:(1)把所给的参数方程利用同角三角函数的基本关系消去参数,化为普通方程.由普通方程判断表示的曲线.
(2)设Q(8cosθ,3sinθ),由中点公式求得M的坐标,根据点M到直线C3 的距离为 d=
=|
sin(θ+
)+4
-1|,当sin(θ+
)=-1时等号成立,即d取得最小值.
(2)设Q(8cosθ,3sinθ),由中点公式求得M的坐标,根据点M到直线C3 的距离为 d=
|3cosθ-2+
| ||||
| 2 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
解答:
解:(1)对于曲线C1:
(t为参数),利用同角三角函数的基本关系消去参数t,可得 (x+4)2+(y-3)2=1;表示以(-4,3)为圆心,1为半径的圆;
对于曲线 C2:
(θ为参数),利用同角三角函数的基本关系消去参数θ,可得
+
=1.表示焦点在x轴上的一个椭圆.
(2)若C1上的点P对应的参数为t=
,则点P的坐标为(-4,4),
设Q(6cosθ,2sinθ)为C2上的动点,则PQ中点M( 3cosθ-2,sinθ+2).
直线C3:
(t为参数)即 x+
y+6
=0.
∴点M到直线C3:x+
y+6
=0的距离为 d=
=|
sin(θ+
)+4
-1|≥3
-1.
当sin(θ+
)=-1时等号成立;所以d的最小值为3
-1
|
对于曲线 C2:
|
| x2 |
| 36 |
| y2 |
| 4 |
(2)若C1上的点P对应的参数为t=
| π |
| 2 |
设Q(6cosθ,2sinθ)为C2上的动点,则PQ中点M( 3cosθ-2,sinθ+2).
直线C3:
|
| 3 |
| 3 |
∴点M到直线C3:x+
| 3 |
| 3 |
|3cosθ-2+
| ||||
| 2 |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
当sin(θ+
| π |
| 3 |
| 3 |
点评:本题主要考查把参数方程化为普通方程的方法,中点公式、点到直线的距离公式的应用,辅助角公式、正弦函数的最值,属于中档题.

练习册系列答案
相关题目
如图所示,程序框图(算法流程图)的输出结果是( )
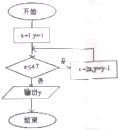

| A、0 | B、-1 | C、-2 | D、-3 |
 如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若
如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若