题目内容
点（a，b）在直线2x-y+3=0的右下方，则（ ）
| A、2a-b+3＜0 |
| B、2a-b+3＞0 |
| C、2a-b+3=0 |
| D、以上都不成立 |
考点：二元一次不等式的几何意义
专题：不等式的解法及应用
分析：点（0，0）在直线2x-y+3=0的右下方区域，代入直线左侧的代数式后大于0，点（a，b）和（0，0）在直线的同侧，所以点的坐标代入直线左侧的代数式后大于0．
解答：
解：点（a，b）在直线2x-y+3=0的右下方
则2a-b+3＞0，
故选B．
则2a-b+3＞0，
故选B．
点评：本题考查了二元一次不等式（组）与平面区域，平面中的直线把平面分成三个部分，直线上的点代入方程成立，直线同侧的点代入直线左侧得到的值同号，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
在跳水比赛中，七位裁判为一选手打出的分数如下：9.0，8.9，9.0，9.5，9.3，9.4，9.3，去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为（ ）
| A、9.2，0.02 |
| B、9.2，0.028 |
| C、9.3，0.02 |
| D、9.3，0.028 |
已知△ABC中，点D在BC边上，且
=4
=r
+s
，则3r+s=（ ）
| CD |
| DB |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
若关于x，y的方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线，则方程（x+cosα）2+（y+sinα）2=1所表示的圆的圆心在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中，A，B，C所对的边分别是a，b，c，满足3a2+3b2=c2+4ab，现设f（x）=tanx，则（ ）
| A、f（sinA）≤f（cosB） |
| B、f（sinA）≥f（cosB） |
| C、f（sinA）≤f（sinB） |
| D、f（cosA）≤f（cosB） |
若向量
，
，
两两所成的角相等，且|
|=|
|=|
|=1，则|
+
+
|=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、0 | ||
| B、3 | ||
| C、3或 0 | ||
D、1或
|
已知A={x|
＞1}，B={x||x|＜a}，若∅?B⊆A，则实数a的取值范围是（ ）
| 4 |
| x+1 |
| A、a＜1 | B、a≤1 |
| C、1≤a≤3 | D、0＜a≤1 |
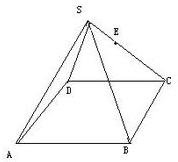在底面是菱形的四棱锥S-ABCD中，SA=SC=2a，SB=SD=