题目内容
若向量
,
,
两两所成的角相等,且|
|=|
|=|
|=1,则|
+
+
|=( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、0 | ||
| B、3 | ||
| C、3或 0 | ||
D、1或
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由于向量
,
,
两两所成的角相等,可知:夹角为0°或120°.分类讨论,利用数量积的性质即可得出.
| a |
| b |
| c |
解答:
解:∵向量
,
,
两两所成的角相等,∴夹角为0°或120°.
当夹角为0°时,又∵|
|=|
|=|
|=1,
∴
•
=
•
=
•
=1×1×cos0°=1,
∴|
+
+
|=
=
=3,
当夹角为120°时,又∵|
|=|
|=|
|=1,
∴
•
=
•
=
•
=1×1×cos120°=-
,
∴|
+
+
|=
=
=0.
综上可得:答案为3或0.
故选:C.
| a |
| b |
| c |
当夹角为0°时,又∵|
| a |
| b |
| c |
∴
| a |
| b |
| a |
| b |
| b |
| c |
∴|
| a |
| b |
| c |
|
| 12×3+2×1×3 |
当夹角为120°时,又∵|
| a |
| b |
| c |
∴
| a |
| b |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
∴|
| a |
| b |
| c |
|
12×3+2×(-
|
综上可得:答案为3或0.
故选:C.
点评:本题考查了向量的夹角、分类讨论、数量积的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=(
)x-log2x,若实数x0是函数f(x)的零点,且0<x<x0,则函数f(x)的值( )
| 1 |
| 3 |
| A、等于0 | B、恒为正 |
| C、恒为负 | D、不大于0 |
执行如图所示的程序框图,若输出的k=6,则输入的整数p的最大值为( )
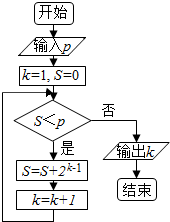

| A、7 | B、15 | C、31 | D、63 |
长方体的一个顶点上三条棱长分别是1、2、3,且它的8个顶点都在同一球面上,则这个球的表面积是( )
| A、7π | B、14π |
| C、28π | D、56π |
点(a,b)在直线2x-y+3=0的右下方,则( )
| A、2a-b+3<0 |
| B、2a-b+3>0 |
| C、2a-b+3=0 |
| D、以上都不成立 |
 如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.
如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.