题目内容
函数y=x-
的大致图象为( )
| 3 | x |
A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:先判断函数为奇函数,排除CD,再根据函数值的特点排除B,问题得以解决
解答:
解:∵f(x)=x-
,
∴f(-x)=-x-
=-(x-
)=-f(x)
∴f(x)为奇函数,
∴图象关于原点对称,故排除C.D
当x趋向于+∞时,y趋向于+∞,故排除B
故选:A
| 3 | x |
∴f(-x)=-x-
| 3 | -x |
| 3 | x |
∴f(x)为奇函数,
∴图象关于原点对称,故排除C.D
当x趋向于+∞时,y趋向于+∞,故排除B
故选:A
点评:本题考查了函数的图象的识别,根据函数的奇偶性单调性定义域和函数值是常用的方法

练习册系列答案
相关题目
设实数a>1,b>1,如下四个结论:
①若lna+2a=lnb+3b,则a>b;
②若lna+2a=lnb+3b,则a<b;
③若lna-2a=lnb-3b,则a>b;
④若lna-2a=lnb-3b,则a<b.
则下列命题成立的是( )
①若lna+2a=lnb+3b,则a>b;
②若lna+2a=lnb+3b,则a<b;
③若lna-2a=lnb-3b,则a>b;
④若lna-2a=lnb-3b,则a<b.
则下列命题成立的是( )
| A、①④ | B、②③ | C、①③ | D、②④ |
已知变量x,y,满足约束条件
,则z=3x+y的最大值为( )
|
| A、3 | ||
| B、12 | ||
C、
| ||
| D、10 |
不等式组
围成的区域为Ω,能够把区域Ω的周长和面积同时分为相等两部分的曲线为( )
|
| A、y=x3-3x+1 | ||
| B、y=xsin2x | ||
C、y=ln
| ||
D、y=
|
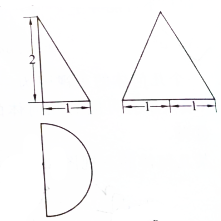 某几何体的三视图如图所示,其正视图是直角三角形,侧视图是等腰三角形,俯视图是半圆.
某几何体的三视图如图所示,其正视图是直角三角形,侧视图是等腰三角形,俯视图是半圆.