题目内容
不等式组
围成的区域为Ω,能够把区域Ω的周长和面积同时分为相等两部分的曲线为( )
|
| A、y=x3-3x+1 | ||
| B、y=xsin2x | ||
C、y=ln
| ||
D、y=
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:画出平面区域,发现Ω是关于原点中心对称的菱形,所以只要在选项中找出是奇函数的即可.
解答:
解:由题意Ω对应的区域如图,
Ω是关于关于原点成中心对称的菱形,
所以能够把区域Ω的周长和面积同时分为相等两部分的曲线对应的函数为奇函数,
选项A是非奇非偶的函数,B是偶函数,D是偶函数;
故选C.

Ω是关于关于原点成中心对称的菱形,
所以能够把区域Ω的周长和面积同时分为相等两部分的曲线对应的函数为奇函数,
选项A是非奇非偶的函数,B是偶函数,D是偶函数;
故选C.
点评:本题考查了二元一次不等式组表示的平面区域的画法以及与函数奇偶性的结合;关键是明确能够把区域Ω的周长和面积同时分为相等两部分的曲线对应的函数的实质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x-
的大致图象为( )
| 3 | x |
A、 |
B、 |
C、 |
D、 |
已知双曲线C:
-
=1的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=asinx+blog2(x+
)+4(a、b为常数),若f(x)在(0,+∞)上有最小值-4,则f(x)在(-∞,0)上有( )
| x2+1 |
| A、最大值-2 |
| B、最大值 4 |
| C、最大值10 |
| D、最大值12 |
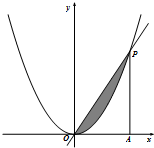 如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为
如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为