题目内容
函数f(x)=
x3-alnx-x2在区间(1,3)内不存在极值点,则a的取值范围是 .
| 1 |
| 3 |
考点:利用导数研究函数的极值
专题:导数的概念及应用
分析:函数f(x)=
x3-alnx-x2(a∈R)在(1,3)内不存在极值点?函数f(x)在(1,3)内单调?函数f′(x)≥0或f′(x)≤0a∈R)在(1,3)内恒成立.再利用导数的运算法则、分离参数法、函数的单调性即可得出.
| 1 |
| 3 |
解答:
解:函数f(x)=
x3-alnx-x2(a∈R)在(1,3)内不存在极值点
?函数f(x)=
x3-alnx-x2(a∈R)在(1,3)内单调
?函数f′(x)≥0或f′(x)≤0a∈R)在(1,3)内恒成立.
由f′(x)=x2-
-2x≥0在(1,3)内恒成立
?a≤(x3-2x2)min,x∈(1,3).即a≤-
,
由f′(x)=x2-
-2x≤0在(1,3)内恒成立
?a≥(x3-2x2)max,x∈(1,3).即a≥9,
故答案为:a≤-
或a≥9.
| 1 |
| 3 |
?函数f(x)=
| 1 |
| 3 |
?函数f′(x)≥0或f′(x)≤0a∈R)在(1,3)内恒成立.
由f′(x)=x2-
| a |
| x |
?a≤(x3-2x2)min,x∈(1,3).即a≤-
| 32 |
| 27 |
由f′(x)=x2-
| a |
| x |
?a≥(x3-2x2)max,x∈(1,3).即a≥9,
故答案为:a≤-
| 32 |
| 27 |
点评:本题考查了利用导数研究函数的单调性极值与最值、分离参数法、函数的单调性等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
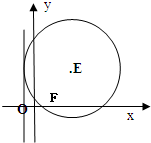 动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.
动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C. 如图,在△AOB中,点P是AB的中垂线上的一点,|
如图,在△AOB中,点P是AB的中垂线上的一点,|