题目内容
已知实数a，b满足b2-（4+i）b+4+ai=0
（1）求a，b的值；
（2）若z∈C且|
-a-bi|-|z|=0，求|z|最小时的复数z．
（1）求a，b的值；
（2）若z∈C且|
. |
| z |
考点：复数求模
专题：数系的扩充和复数
分析：（1）由条件利用两个复数相等的充要条件求出a，b的值．
（2）设z=x+yi，x、y∈R，由题意可得|（x-2）+（-y-2）i|=|x+yi|，化简可得x-y=2．再根据|z|=
=
，求得|z|的最小值以及此时对应的z值．
（2）设z=x+yi，x、y∈R，由题意可得|（x-2）+（-y-2）i|=|x+yi|，化简可得x-y=2．再根据|z|=
| x2+y2 |
| 2(x-1)2+2 |
解答：
解：（1）∵实数a，b满足b2-（4+i）b+4+ai=0，∴b2-4b+4=0，a-b=0，
求得a=b=2．
（2）|
-a-bi|-|z|=0，即|
-2-2i|-|z|=0，
设z=x+yi，x、y∈R，则有|（x-2）+（-y-2）i|=|x+yi|，
即 （x-2）2+（y+2）2=x2+y2，化简可得x-y=2．
∴|z|=
=
=
，故当x=1时，|z|最小，此时，y=-1，
故此时z=1-i．
求得a=b=2．
（2）|
. |
| z |
. |
| z |
设z=x+yi，x、y∈R，则有|（x-2）+（-y-2）i|=|x+yi|，
即 （x-2）2+（y+2）2=x2+y2，化简可得x-y=2．
∴|z|=
| x2+y2 |
| 2x2-4x+4 |
| 2(x-1)2+2 |
故此时z=1-i．
点评：本题主要考查两个复数相等的充要条件，复数求模的方法，二次函数的最值，属于基础题．
练习册系列答案
相关题目
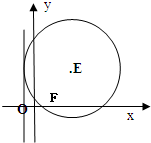动圆E过点F（1，0），且与直线x=-1相切，圆心E的轨迹是曲线C．