题目内容
sin220°+cos250°+sin20°cos50°= .
考点:二倍角的余弦,二倍角的正弦
专题:三角函数的求值
分析:先根据二倍角公式降幂,再由积化和差公式、和和差化积化简即可得到答案.
解答:
解:sin220°+cos250°+sin20°cos50°=
(1-cos40°)+
(1+cos100°)+sin20°cos50°
=1+
(cos100°-cos40°)+
(sin70°-sin30°)=
+
×(-2)sin70°sin30°+
sin70°
=
,
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查二倍角公式、积化和差公式、和和差化积公式的应用,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知函数f(x)=xlnx,若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
| A、x+y-1=0 |
| B、x-y-1=0 |
| C、x+y+1=0 |
| D、x-y+1=0 |
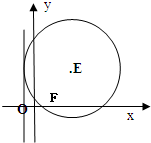 动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.
动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C. 如图:通过以“直”代“曲”无限逼近的方法求曲边梯形的面积的步骤是
如图:通过以“直”代“曲”无限逼近的方法求曲边梯形的面积的步骤是