题目内容
15.在正方体ABCD-A1B1C1D1中,E是棱D1C1的中点,则异面直线D1B、EC的夹角的余弦值为( )| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{15}}}{5}$ |
分析 如图所示,建立空间直角坐标系.不妨设AB=2.利用$cos<\overrightarrow{B{D}_{1}},\overrightarrow{CE}>$=$\frac{\overrightarrow{B{D}_{1}}•\overrightarrow{CE}}{|\overrightarrow{B{D}_{1}}||\overrightarrow{CE}|}$即可得出.
解答 解:如图所示,建立空间直角坐标系.
不妨设AB=2.
D(0,0,0),B(2,2,0),C(0,2,0),E(0,1,2),D1=(0,0,2).
$\overrightarrow{B{D}_{1}}$=(-2,-2,2),$\overrightarrow{CE}$=(0,-1,2),
∴$cos<\overrightarrow{B{D}_{1}},\overrightarrow{CE}>$=$\frac{\overrightarrow{B{D}_{1}}•\overrightarrow{CE}}{|\overrightarrow{B{D}_{1}}||\overrightarrow{CE}|}$=$\frac{2+4}{\sqrt{12}×\sqrt{5}}$=$\frac{\sqrt{15}}{5}$.
∴异面直线D1B、EC的夹角的余弦值为$\frac{\sqrt{15}}{5}$.
故选:D.
点评 本题考查了向量夹角公式、数量积运算性质、异面直线所成的角,考查了推理能力与就你死了,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知向量$\overrightarrow a=({1,3})$,$\overrightarrow b=({-2,m})$,若$\overrightarrow a$与$\overrightarrow a+2\overrightarrow b$平行,则m的值为( )
| A. | 1 | B. | -1 | C. | -2 | D. | -6 |
6.点(x,y)满足$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤4\\ x,y∈N\end{array}\right.$,则点A落在区域C:x2+y2-4x-4y+7≤0内的概率为( )
| A. | $\frac{π}{16}$ | B. | $\frac{5}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
3.已知由不等式$\left\{{\begin{array}{l}{x≥y}\\{y≥0}\\{x+y-4≤0}\end{array}}\right.$所确定的平面区域为M,由不等式x2+y2≤8所确定的平面区域为N,区域M内随机抽取一个点,该点同时落在区域N内的概率是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{16}$ | D. | $\frac{π}{4}$ |
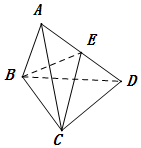 如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.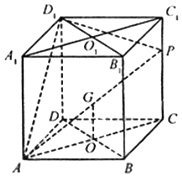 如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,