题目内容
7.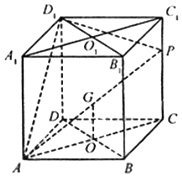 如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为$4\sqrt{2}$;
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.
分析 (1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点,连接OG,证明AO⊥平面BDD1B1,说明∠AGO是AP与平面BDD1B1所成的角.在Rt△AOG中,利用直线AP与平面BDD1B1所成的角的正切值为4$\sqrt{2}$.求出m的值.
(2)点Q应当是AICI的中点,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,通过证明 D1O1⊥平面ACC1A1,D1O1⊥AP.利用三垂线定理推出结论.
解答 解:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G,
连接OG,因为PC∥平面BDD1B1,平面BDD1B1∩平面APC=OG,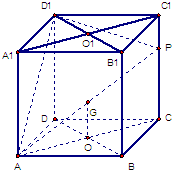
故OG∥PC,所以,OG=$\frac{1}{2}$PC=$\frac{m}{2}$.
又AO⊥BD,AO⊥BB1,所以AO⊥平面BDD1B1,
故∠AGO是AP与平面BDD1B1所成的角.
在Rt△AOG中,tan∠AGO=$\frac{\frac{\sqrt{2}}{2}}{\frac{m}{2}}=4\sqrt{2}$,即m=$\frac{1}{4}$.
所以,当m=$\frac{1}{4}$时,直线AP与平面BDD1B1所成的角的正切值为4$\sqrt{2}$.
(2)可以推测,点Q应当是AICI的中点,当是中点时
因为D1O1⊥A1C1,且 D1O1⊥A1A,A1C1∩A1A=A1,
所以 D1O1⊥平面ACC1A1,
又AP?平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直.
点评 本题考查直线与平面所成的角,考查直线与平面垂直的判定,三垂线定理的应用,考查空间想象能力,逻辑推理能力.

练习册系列答案
相关题目
15.在正方体ABCD-A1B1C1D1中,E是棱D1C1的中点,则异面直线D1B、EC的夹角的余弦值为( )
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{15}}}{5}$ |
12.一次考试中,5名学生的数学、物理成绩如下:
求y关于x的线性回归方程.
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
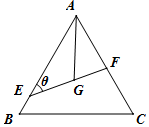 如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.
如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.