题目内容

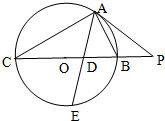如图，△ABC内接于直径为BC的圆O，过点A作圆O的切线交CB的延长线于点P，∠BAC的平分线分别交BC和圆O于点D、E，若PA=2PB=10．
（1）求证：AC=2AB；
（2）求AD•DE的值．
考点：相似三角形的判定
专题：推理和证明
分析：（1）通过证明△ABP∽△CAP，然后证明AC=2AB；
（2）利用切割线定理以及相交弦定理直接求AD•DE的值．
解答： 解：（1）∵PA是圆O的切线∴∠PAB=∠ACB又∠P是公共角
∴△ABP∽△CAP…（2分）
∴
AC
AB
=
AP
PB
=2∴AC=2AB…（4分）
（2）由切割线定理得：PA2=PB•PC∴PC=20
又PB=5∴BC=15…（6分）
又∵AD是∠BAC的平分线∴
AC
AB
=
CD
DB
=2
∴CD=2DB∴CD=10，DB=5…（8分）
又由相交弦定理得：AD•DE=CD•DB=50…（10分）
点评：本题主要考查与圆有关的比例线段、相似三角形的判定及切线性质的应用．属于基础题．
练习册系列答案
相关题目
A、B是单位圆O上的点，点A是单位圆与x轴正半轴的交点，点B在第二象限．记∠AOB=θ且sinθ=
4
5
．
（1）求B点坐标；
（2）求
sin(π+θ)+2sin(
π
2
-θ)
2cos(π-θ)
的值．
当0＜x≤
1
2
时，4x＜logax，则a的取值范围是（　　）
A、（
2
，2）
B、（1，
2
）
C、（
2
2
，1）
D、（0，
2
2
）
下列说法正确的是（　　）
A、三点确定一个平面
B、四边形一定是平面图形
C、梯形一定是平面图形
D、平面α和平面β有不同在一条直线上的三个公共点
已知双曲线
x2
a2
-
y2
3
=1（a＞0）的离心率为2，则实数a=（　　）
A、2
B、
6
2
C、
5
2
D、1
给出下列四个推导过程：
①∵a，b∈R+，∴（
b
a
）+（
a
b
）≥2
lgxlgy
=2；
②∵x，y∈R+，∴lgx+lgy≥2
lgxlgy
；
③∵a∈R，a≠0，∴（
4
a
）+a≥2
4
a
•a
=4；
④∵x，y∈R，xy＜0，∴（
x
y
）+（
y
x
）=-[（-（
x
y
））+（-（
y
x
））]≤-2
(-
x
y
)(-
y
x
)
=-2．
其中正确的是（　　）
A、①②B、②③C、③④D、①④
已知f（x）=x3+ax2+bx+c，在x=1与x=-2时，都取得极值．
（Ⅰ）求a，b的值；
（Ⅱ）若x∈[-3，2]都有f（x）＞
4
c
-
1
2
，（c＞0）恒成立，求c的取值范围．
已知向量
a
和
b
的夹角为60°，|
a
|=10，|
b
|=8，求：
（1）|
a
+
b
|；
（2）
a
+
b
与
a
的夹角θ的余弦值．
已知二次函数f（x）的二次项系数为a，且不等式f（x）＞-4x的解集为（1，3）．
（1）若方程f（x）+6a=0有两个相等的实根，求f（x）的解析式；
（2）若f（x）的最大值为正数，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网