题目内容
当0<x≤
时,4x<logax,则a的取值范围是( )
| 1 |
| 2 |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
D、(0,
|
考点:对数函数的图像与性质,指数函数的图像与性质
专题:函数的性质及应用
分析:若当0<x≤
时,不等式4x<logax恒成立,则在当0<x≤
时,y=logax的图象恒在y=4x的图象的上方,在同一坐标系中,分析画出指数和对数函数的图象,分析可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:当0<x≤
解:当0<x≤
时,函数y=4x的图象如下图所示
若不等式4x<logax恒成立,则y=logax的图象恒在y=4x的图象的上方(如图中虚线所示)
∵y=logax的图象与y=4x的图象交于(
,2)点时,a=
故虚线所示的y=logax的图象对应的底数a应满足
<a<1,
故选:C
 解:当0<x≤
解:当0<x≤| 1 |
| 2 |
若不等式4x<logax恒成立,则y=logax的图象恒在y=4x的图象的上方(如图中虚线所示)
∵y=logax的图象与y=4x的图象交于(
| 1 |
| 2 |
| ||
| 2 |
故虚线所示的y=logax的图象对应的底数a应满足
| ||
| 2 |
故选:C
点评:本题以指数函数与对数函数图象与性质为载体考查了函数恒成立问题,其中熟练掌握指数函数和对数函数的图象与性质是解答本题的关键

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知q是等比数列{an}的公比,则“q<1”是“数列{an}是递减数列”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
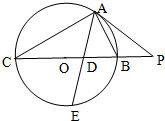 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.