题目内容
已知函数g（x）=2x-2+1，求g-1（x）．
考点：反函数
专题：函数的性质及应用
分析：由原函数的解析式求出x，再把x、y互换，即可得到原函数的反函数，并注明反函数的定义域（即原函数的值域）．
解答：
解：根据y=g（x）=2x-2+1，可得y-1=2x-2，
即 x-2=log2（y-1），
即 x=log2（y-1）+2=log2（4y-4），
故g-1（x）=log2（4x-4），（ x＞1）．
即 x-2=log2（y-1），
即 x=log2（y-1）+2=log2（4y-4），
故g-1（x）=log2（4x-4），（ x＞1）．
点评：本题主要考查求一个函数的反函数的方法，属于基础题．
练习册系列答案
相关题目
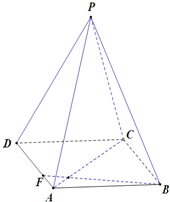如图所示，正四棱锥P=ABCD中，AB=1，侧棱PA与底面ABCD所成角的正切值为
根据如图所示算法语句，将输出的A值依次分别记为a1，a2，…，an，…，a2014