题目内容
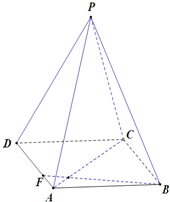 如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为
如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为
| ||
| 2 |
(1)求二面角P-CD-A的大小.
(2)设点F在AD上,AF=
| 1 |
| 3 |
考点:点、线、面间的距离计算,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(1)连结AC、BD交于点O,连结PO,则PO⊥平面ABCD,∠PAO就是PA与底面ABCD所成的角,设E为CD的中点,连结PE、OE,∠PEO就是二面角P-CD-AD的平面角,由此能求出二面角P-CD-A的大小.
(2)过O作OM⊥BF于M,连结PM,则由于PO⊥平面ABCD,PM⊥BF,作OH⊥PM于H,OH的长就等于点O到平面PBF的距离,由此能求出点A到到平面PBF的距离.
(2)过O作OM⊥BF于M,连结PM,则由于PO⊥平面ABCD,PM⊥BF,作OH⊥PM于H,OH的长就等于点O到平面PBF的距离,由此能求出点A到到平面PBF的距离.
解答:
解:(1)连结AC、BD交于点O,连结PO,则PO⊥平面ABCD
∴∠PAO就是PA与底面ABCD所成的角,tan∠PAO=
,
PO=AO•tan∠PAO=
,
设E为CD的中点,连结PE、OE,
则OE⊥CD,PE⊥CD,
∴∠PEO就是二面角P-CD-AD的平面角,
在Rt△PEO中,tan∠PAO=
=1,
即∠PAO=
,
∴二面角P-CD-A的大小为
.
(2)过O作OM⊥BF于M,
连结PM,则由于PO⊥平面ABCD,PM⊥BF,
∴BF⊥平面POM,平面POM⊥平面PBF,作OH⊥PM于H,
则OH⊥平面PBF,
即OH的长就等于点O到平面PBF的距离,
∵AF=
AD=
BC,设AC与BF交于点N,
则AN=
NC,AN=NO
∴点A到平面PBF的距离就等于点O到平面PBF的距离,
作AQ⊥BF于Q,则AQ=OM=
,
在Rt△PMH中,OH=
=
,
故点A到到平面PBF的距离为
.
∴∠PAO就是PA与底面ABCD所成的角,tan∠PAO=
| ||
| 2 |
PO=AO•tan∠PAO=
| 1 |
| 2 |
设E为CD的中点,连结PE、OE,
则OE⊥CD,PE⊥CD,
∴∠PEO就是二面角P-CD-AD的平面角,
在Rt△PEO中,tan∠PAO=
| PO |
| OE |

即∠PAO=
| π |
| 4 |
∴二面角P-CD-A的大小为
| π |
| 4 |
(2)过O作OM⊥BF于M,
连结PM,则由于PO⊥平面ABCD,PM⊥BF,
∴BF⊥平面POM,平面POM⊥平面PBF,作OH⊥PM于H,
则OH⊥平面PBF,
即OH的长就等于点O到平面PBF的距离,
∵AF=
| 1 |
| 3 |
| 1 |
| 3 |
则AN=
| 1 |
| 3 |
∴点A到平面PBF的距离就等于点O到平面PBF的距离,
作AQ⊥BF于Q,则AQ=OM=
| ||
| 10 |
在Rt△PMH中,OH=
| PO•OM |
| PM |
| ||
| 14 |
故点A到到平面PBF的距离为
| ||
| 14 |
点评:本题考查二面角的大小的求法,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 若函数f(x)=Asin(2x+φ)(A>0,-
若函数f(x)=Asin(2x+φ)(A>0,-| π |
| 2 |
| π |
| 2 |
| A、-2 | ||
| B、-1 | ||
C、-
| ||
D、-
|
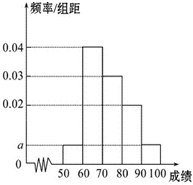 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]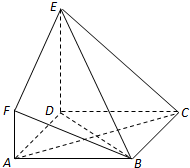 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.