题目内容
已知：在数列{an}中，a1=7，an+1=
，
（1）请写出这个数列的前4项，并猜想这个数列的通项公式．
（2）请证明你猜想的通项公式的正确性．
| 7an |
| an+7 |
（1）请写出这个数列的前4项，并猜想这个数列的通项公式．
（2）请证明你猜想的通项公式的正确性．
考点：数学归纳法,数列的概念及简单表示法
专题：综合题,点列、递归数列与数学归纳法
分析：（1）由a1=7，an+1=
，代入计算，可求数列的前4项，从而猜想{an}的通项公式；
用数学归纳法证明，关键是假设当n=k（k≥1）时，命题成立，利用递推式，证明当n=k+1时，等式成立．
| 7an |
| an+7 |
用数学归纳法证明，关键是假设当n=k（k≥1）时，命题成立，利用递推式，证明当n=k+1时，等式成立．
解答：
解：（1）由已知a1=7，a2=
，a3=
，a4=
…（3分）
猜想：an=
…（6分）
（2）由an+1=
两边取倒数得：?
=
+
，?
-
=
，…（9分）
?数列 {
}是以
=
为首相，以
为公差的等差数列，…（12分）
⇒
=
+（n-1）
=
?a n=
…（14分）
| 7 |
| 2 |
| 7 |
| 3 |
| 7 |
| 4 |
猜想：an=
| 7 |
| n |
（2）由an+1=
| 7an |
| an+7 |
两边取倒数得：?
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 7 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 7 |
?数列 {
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 7 |
| 1 |
| 7 |
⇒
| 1 |
| an |
| 1 |
| 7 |
| 1 |
| 7 |
| n |
| 7 |
| 7 |
| n |
点评：本题考查猜想、证明的推理方法，考查数学归纳法证明命题．注意证明的步骤的应用．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
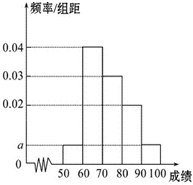某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
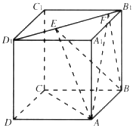如图，正方体ABCD-A1B1C1D1的棱线长为1，线段B1D1上有两个动点E，F，且EF=