题目内容
设等差数列{an}的第11项为20,第25项为-22,求:
(1)数列{an}的通项公式;
(2)数列{an}前50项的绝对值之和.
(1)数列{an}的通项公式;
(2)数列{an}前50项的绝对值之和.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式求出a1=50,d=-3,由此能求出an=53-3n.
(2)由a1=50,d=-3,求出Sn=-
n2+
n.设数列{an}前50项的绝对值之和为Tn.当n≤17时,Tn=Sn;当n≥18时,Tn=-Sn+2S17.由此能求出数列{an}前50项的绝对值之和.
(2)由a1=50,d=-3,求出Sn=-
| 3 |
| 2 |
| 103 |
| 2 |
解答:
解:(1)∵等差数列{an}的第11项为20,第25项为-22,
∴
,解得a1=50,d=-3,
∴an=50+(n-1)×(-3)=53-3n.
(2)∵a1=50,d=-3,
∴Sn=50n+
×(-3)=-
n2+
n.
由an=53-3n≥0,得n≤
,
设数列{an}前n项的绝对值之和为Tn.
当n≤17时,Tn=Sn=-
n2+
n.
当n≥18时,Tn=-Sn+2S17=
n2-
n+884.
∴数列{an}前50项的绝对值之和:
T50=
×2500-
×50+884=2059.
∴
|
∴an=50+(n-1)×(-3)=53-3n.
(2)∵a1=50,d=-3,
∴Sn=50n+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 103 |
| 2 |
由an=53-3n≥0,得n≤
| 53 |
| 3 |
设数列{an}前n项的绝对值之和为Tn.
当n≤17时,Tn=Sn=-
| 3 |
| 2 |
| 103 |
| 2 |
当n≥18时,Tn=-Sn+2S17=
| 3 |
| 2 |
| 103 |
| 2 |
∴数列{an}前50项的绝对值之和:
T50=
| 3 |
| 2 |
| 103 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列{an}前50项的绝对值之和,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
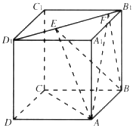 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=