题目内容
等比数列的前三项为a,2a+2,3a+3,问这个数列的第几项的值为-
?
| 81 |
| 4 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由等比中项可得a(3a+3)=(2a+2)2.解得a=-1,或a=-4,当a=-1时,矛盾;当a=-4时,求通项,验证可得.
解答:
解:∵a,2a+2,3a+3是等比数列的前三项,
∴a(3a+3)=(2a+2)2.
解得a=-1,或a=-4.
当a=-1时,数列的前三项依次为-1,0,0,与等比数列定义矛盾,故a=-1舍去;
当a=-4时,数列的前三项依次为-4,-6,-9,
则公比为q=
,∴an=-4(
)n-1,
令-4(
)n-1=-
,
∴n-1=4,即n=5,
∴-
是这个数列中的第5项.
∴a(3a+3)=(2a+2)2.
解得a=-1,或a=-4.
当a=-1时,数列的前三项依次为-1,0,0,与等比数列定义矛盾,故a=-1舍去;
当a=-4时,数列的前三项依次为-4,-6,-9,
则公比为q=
| 3 |
| 2 |
| 3 |
| 2 |
令-4(
| 3 |
| 2 |
| 81 |
| 4 |
∴n-1=4,即n=5,
∴-
| 81 |
| 4 |
点评:本题考查等比数列的性质和通项公式,涉及分类讨论的思想,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
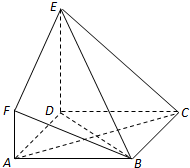 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.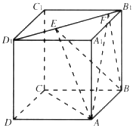 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=