题目内容
19.已知等差数列{an}的公差d=2,前n项和为Sn,等比数列{bn}满足b1=a1,b2=a4,b3=a13(1)求an,bn;
(2)记数列$\left\{{\frac{1}{S_n}}\right\}$的前n项和为Tn,求Tn.
分析 (1)等比数列{bn}满足b1=a1,b2=a4,b3=a13.可得${a}_{4}^{2}$=a1a13,$({a}_{1}+3×2)^{2}$=a1(a1+12×2),解得a1.再利用等差数列与等比数列的通项公式即可得出.
(2)Sn=n(n+2).可得$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$.利用“裂项求和”方法即可得出.
解答 解:(1)等比数列{bn}满足b1=a1,b2=a4,b3=a13.
∴${a}_{4}^{2}$=a1a13,d=2.
∴$({a}_{1}+3×2)^{2}$=a1(a1+12×2),解得a1=3.
∴an=3+2(n-1)=2n+1.
公比q=$\frac{{a}_{4}}{{a}_{1}}$=$\frac{2×4+1}{3}$=3.
∴bn=3n.
(2)Sn=$\frac{n(3+2n+1)}{2}$=n(n+2).
∴$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$.
∴Tn=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})$+$(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}$$(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| 理科 | 文科 | |
| 男 | 14 | 10 |
| 女 | 6 | 20 |
(2)利用列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为选修文理科与性别有关?
| A. | 6 | B. | -6 | C. | 0 | D. | $\frac{1}{6}$ |
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | -3 | D. | 3 |
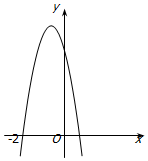 已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.
已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.