题目内容
9.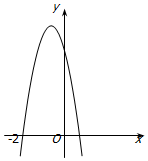 已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.
已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数y=f(x)在区间[-3,2]上的最大值与最小值.
分析 (Ⅰ)根据题意可知函数在x=-2处取极小值8,由此列出方程组求出a和b,由此能求出f(x)的解析式.
(Ⅱ)由f′(x)=-3x2-4x+4=0,得${x}_{1}=\frac{2}{3}$,x2=-2,由此能求出函数y=f(x)在区间[-3,2]上的最大值,最小值.
解答 解:(Ⅰ)根据题意可知函数在x=-2处取极小值8,
∵f(x)=ax3+bx2+4x,
∴f′(x)=3ax2+2bx+4
∴$\left\{\begin{array}{l}{{f}^{'}(-2)=12a-4b+4=0}\\{f(-2)=-8a+4b-8=-8}\end{array}\right.$,
解得:a=-1,b=-2
∴f(x)=-x3-2x2+4x.
(Ⅱ)由(Ⅰ)得f′(x)=-3x2-4x+4,
由f′(x)=0,得${x}_{1}=\frac{2}{3}$,x2=-2,
∵f(-3)=-(-3)3-2(-3)2+4(-3)=-3,
f(-2)=-(-2)3-2(-2)2+4(-2)=-8,
f($\frac{2}{3}$)=-($\frac{2}{3}$)3-2($\frac{2}{3}$)2+4×$\frac{2}{3}$=-$\frac{8}{27}$,
f(2)=-23-2•22+4•2=8.
∴函数y=f(x)在区间[-3,2]上的最大值为8,最小值为-8.
点评 本题考查函数的解析式的求法,考查函数的最大值、最小值的求法,考查导数的应用,考查推理论证能力、运算求解能力,考查转化化归思想、分类讨论思想,是中档题.

练习册系列答案
相关题目
19.若正方形ABCD边长为2,E为边上任意一点,则AE的长度大于$\sqrt{5}$的概率等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
20.设x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$,则目标函数z=$\frac{x+2y-1}{x+1}$的最大值为( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | 4 |
17.为考察数学成绩与物理成绩的关系,在高二随机抽取了300名学生.得到下面列联表:
附表:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(b+d)(c+d)}$
现判断数学成绩与物理成绩有关系,则判断的出错率为( )
| 数学 物理 | 85~100分 | 85分以下 | 合计 |
| 85~100分 | 37 | 85 | 122 |
| 85分以下 | 35 | 143 | 178 |
| 合计 | 72 | 228 | 300 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
现判断数学成绩与物理成绩有关系,则判断的出错率为( )
| A. | 0.5% | B. | 1% | C. | 2% | D. | 5% |
14.已知命题p:直线l1:x-2y+3=0与l2:2x+y+3=0相交但不垂直;命题q:?x0∈(0,+∞),x0+2>ex0,则下列命题中是真命题的是( )
| A. | (?p)∧q | B. | p∧q | C. | p∨(?q) | D. | (?p)∧(?q) |
1.已知i是虚数单位,复数z=(3+i)(1-i)对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |