题目内容
已知命题p：存在x∈[1，4]使得x2-4x+a=0成立，命题q：对于任意x∈R，函数f（x）=lg（x2-ax+4）恒有意义．
（1）若p是真命题，求实数a的取值范围；
（2）若p∨q是假命题，求实数a的取值范围．
（1）若p是真命题，求实数a的取值范围；
（2）若p∨q是假命题，求实数a的取值范围．
考点：复合命题的真假
专题：计算题
分析：（1）根据函数的根的存在性定理分两类存在一个x∈[1，4]满足条件和存在两个x∈[1，4]满足条件，求出p是真命求实数a的取值范围
（2）本题考查的知识点是复合命题的真假判定，解决的办法是先求出简单命题为真命题的参数范围，再根据真值表进行判断．
（2）本题考查的知识点是复合命题的真假判定，解决的办法是先求出简单命题为真命题的参数范围，再根据真值表进行判断．
解答：
解：（1）设g（x）=x2-4x+a，对称轴为x=2
若存在一个x∈[1，4]满足条件，则g（1）＜0，g（4）≥0，得0≤a＜3，…（3分）
若存在两个x∈[1，4]满足条件，则g（1）≥0，g（2）≤0，得3≤a≤4，
故p是真命题时实数a的取值范围为0≤a≤4…（6分）
（2）由题意知p，q都为假命题，
若p为假命题，则a＜0或a＞4…（8分）
若命题q为真命题即对于任意x∈R，函数f（x）=lg（x2-ax+4）恒有意义
所以x2-ax+4＞0恒成立
所以△=a2-16＜0得-4＜a＜4
所以q为假命题时a≤-4或a≥4…（10分）
故满足条件的实数a的取值范围为a≤-4或a＞4…（12分）
若存在一个x∈[1，4]满足条件，则g（1）＜0，g（4）≥0，得0≤a＜3，…（3分）
若存在两个x∈[1，4]满足条件，则g（1）≥0，g（2）≤0，得3≤a≤4，
故p是真命题时实数a的取值范围为0≤a≤4…（6分）
（2）由题意知p，q都为假命题，
若p为假命题，则a＜0或a＞4…（8分）
若命题q为真命题即对于任意x∈R，函数f（x）=lg（x2-ax+4）恒有意义
所以x2-ax+4＞0恒成立
所以△=a2-16＜0得-4＜a＜4
所以q为假命题时a≤-4或a≥4…（10分）
故满足条件的实数a的取值范围为a≤-4或a＞4…（12分）
点评：本题考查的知识点是复合命题的真假判定，解决的办法是先求出简单命题为真命题的参数范围，属于中档题目．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
在△ABC中，已知sin（
-A）cosB＞sinAsin（π-B），则△ABC是（ ）
| π |
| 2 |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
若直线（2n+1）x+（n+5）y-6=0和（n-3）x+（1-2n）y-7=0垂直，则n的值为（ ）
A、
| ||
B、-
| ||
| C、1 | ||
D、
|
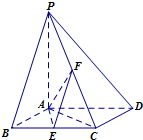如图，已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
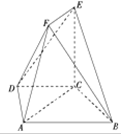如图所示的几何体，四边形ABCD中，有AB∥CD，∠BAC=30°，AB=2CD=2，CB=1．点E在平面ABCD内的射影是点C，EF∥AC，且AC=2EF．
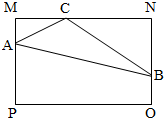如图，已知四边形MNOP是一个矩形，MN=