题目内容
已知圆O：（x-2）2+（y+4）2=2，点P是圆O上的一动点，则
的最大值是 ；
的最小值是 ．
| x2+y2 |
| y |
| x |
考点：圆的标准方程,两点间距离公式的应用
专题：直线与圆
分析：（1）首先求出圆心到原点的距离，进一步求出最大值．
（2）利用直线和圆相切求出最值，进一步求出最小值．
（2）利用直线和圆相切求出最值，进一步求出最小值．
解答：
解：（1）已知圆O：（x-2）2+（y+4）2=2，
O（2，-4），R=
则：
的最大值：
+R=2
+
（2）利用直线和圆的关系：设直线方程为：y=kx
则：当直线与圆相切时：
=
解得：k=-1或-7
所以：
的最小值为：-7
故答案为：2
+
-7
O（2，-4），R=
| 2 |
则：
| x2+y2 |
| (-2)2+42 |
| 5 |
| 2 |
（2）利用直线和圆的关系：设直线方程为：y=kx
则：当直线与圆相切时：
| |-4-2k| | ||
|
| 2 |
解得：k=-1或-7
所以：
| y |
| x |
故答案为：2
| 5 |
| 2 |
点评：本题考查的知识点：与圆有关的最值问题，直线与圆的位置关系．
练习册系列答案
相关题目
已知两个正实数x，y满足
+
=1，并且x+2y≥m2-2m恒成立，则实数m的取值范围是（ ）
| 2 |
| x |
| 1 |
| y |
| A、（-2，4） |
| B、[-2，4] |
| C、（-∞，-2）∪（4，+∞） |
| D、（-∞，-2]∪[4，+∞） |
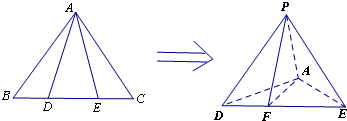
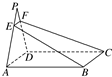如图所示，四边形ABCD是矩形，P∉平面ABCD，过BC作平面BCFE交AP于E，交DP于F．
