题目内容
函数f(x)=2sin
cos(
+
)+
的最大值为 .
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:由三角函数公式化简可得f(x)=sin(x+
),易得当x+
=2kπ+
时,已知函数取最大值1
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:
解:化简可得f(x)=2sin
(cos
cos
-sin
sin
)+
=2sin
(
cos
-
sin
)+
=
•2sin
cos
-sin2
+
=
sinx-
+
=sin(x+
),
∴当x+
=2kπ+
时,已知函数取最大值1
故答案为:1
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
| x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
=2sin
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1-cosx |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴当x+
| π |
| 6 |
| π |
| 2 |
故答案为:1
点评:本题考查三角函数的最值,涉及三角函数的化简,属基础题.

练习册系列答案
相关题目
若a,b,c为实数,且a<b<0,则下列命题正确的是( )
| A、ac2<bc2 | ||||
B、
| ||||
C、
| ||||
| D、a2>ab>b2 |
已知f(x)=
,x∈R,求f(
)+f(
)+f(
)+…+f(
)=( )
| 4x |
| 4x+2 |
| 1 |
| 1001 |
| 2 |
| 1001 |
| 3 |
| 1001 |
| 1000 |
| 1001 |
| A、499.5 | B、500.5 |
| C、500 | D、499 |
函数y=kx+b与函数y=
在同一坐标系中的大致图象正确的是( )
| kb |
| x |
A、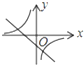 |
B、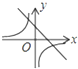 |
C、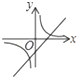 |
D、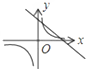 |
函数f(x)=ax-1+2经过定点( )
| A、(2,2) |
| B、(2,3) |
| C、(1,2) |
| D、(1,3) |