题目内容
(如图)正△ABC的边长为3,D、E分别是BC边上的三等分点,沿AD、AE折起,使B、C两点重合于点P,则下列结论:
①AP⊥DE;
②AP与面PDE所成角的正弦值是
;
③P到平面ADE的距离为
;
④AP与底面ADE所成角的余弦值为
.
其中正确结论的序号为 (把你认为正确的序号都填上).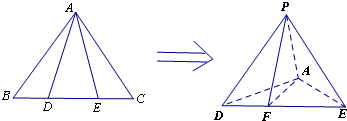
①AP⊥DE;
②AP与面PDE所成角的正弦值是
| ||
| 3 |
③P到平面ADE的距离为
| ||
| 3 |
④AP与底面ADE所成角的余弦值为
| ||
| 9 |
其中正确结论的序号为

考点:命题的真假判断与应用
专题:解三角形,空间位置关系与距离,简易逻辑
分析:取DE的中点F,连接PF,从而可证DE⊥平面AFP,则AP⊥DE;故①正确;
②AP与面PDE所成角为∠APF,先用余弦定理求余弦,再求正弦;
③设P到平面ADE的距离为h,利用三角形面积公式求解;
④AP与底面ADE所成角的为∠PAF,利用余弦定理求余弦.
②AP与面PDE所成角为∠APF,先用余弦定理求余弦,再求正弦;
③设P到平面ADE的距离为h,利用三角形面积公式求解;
④AP与底面ADE所成角的为∠PAF,利用余弦定理求余弦.
解答:
 解:如图,取DE的中点F,连接PF,
解:如图,取DE的中点F,连接PF,
则由题意可得,AF⊥DE,PF⊥DE,
又∵AF∩PF=F,
∴DE⊥平面AFP,
∴AP⊥DE,故①正确;
②AP与面PDE所成角为∠APF,
其中PA=3,AF=
,PF=
;
∴cos∠APF=
=
,
∴sin∠APF=
;故正确;
③设P到平面ADE的距离为h,
则
×3×
×
=
×
×h;
则h=
;故正确;
④AP与底面ADE所成角的为∠PAF,
∴cos∠PAF=
=
,故错误.
故答案为:①②③.
 解:如图,取DE的中点F,连接PF,
解:如图,取DE的中点F,连接PF,则由题意可得,AF⊥DE,PF⊥DE,
又∵AF∩PF=F,
∴DE⊥平面AFP,
∴AP⊥DE,故①正确;
②AP与面PDE所成角为∠APF,
其中PA=3,AF=
3
| ||
| 2 |
| ||
| 2 |
∴cos∠APF=
| AP2+PF2-AF2 |
| 2AP•PF |
| ||
| 3 |
∴sin∠APF=
| ||
| 3 |
③设P到平面ADE的距离为h,
则
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
则h=
| ||
| 3 |
④AP与底面ADE所成角的为∠PAF,
∴cos∠PAF=
| AP2+AF2-PF2 |
| 2•AP•AF |
5
| ||
| 9 |
故答案为:①②③.
点评:本题考查了命题的真假性的判断,同时考查了空间几何体的位置关系及余弦定理的应用,属于难题.

练习册系列答案
相关题目