题目内容
定义max{x1，x2，x3}为实数x1，x2，x3中的较大值，记f（x）=max{sinx，cosx，
}，则f（x）min= ．
| sinx+cosx | ||
|
考点：三角函数的最值,函数单调性的性质
专题：三角函数的图像与性质
分析：根据本题的特点，作出三个函数的图象，利用图象的直观得出所求最小值是正弦函数与余弦函数交点中纵坐标较小的那一个，再由正余弦函数的性质求出值即可
解答：
解：由于
=sin(x+
)，作出三个函数的图象如图
f（x）=max{sinx，cosx，
}的最小值在如图的点A处取到，A点是正弦函数与余弦函数交点中纵坐标较小的那一个
由正余弦函数的性质知，点A的纵坐标是-
故答案为-
| sinx+cosx | ||
|
| π |
| 4 |
f（x）=max{sinx，cosx，
| sinx+cosx | ||
|
由正余弦函数的性质知，点A的纵坐标是-
| ||
| 2 |
故答案为-
| ||
| 2 |
点评：本题考查三角函数的最值，由于涉及到三个函数及一个新定义，情形较复杂，借助图象的直观指引解答相对较易，本题考查了数形结合的思想及利用图形推理判断的能力，好题
练习册系列答案
黄冈冠军课课练系列答案
相关题目
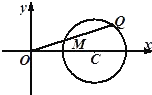（理科）如图，圆C：（x-2）2+y2=1，点Q是圆C上任意一点，M是线段OQ的中点．