题目内容
已知a∈R，函数f（x）=x3-
x+a2，x∈R．
（Ⅰ）求f（x）在[-1，1]上的单调区间；
（Ⅱ）当0＜a＜2时，求|f（x）|在[-1，1]上的最大值．
| 3a |
| 2 |
（Ⅰ）求f（x）在[-1，1]上的单调区间；
（Ⅱ）当0＜a＜2时，求|f（x）|在[-1，1]上的最大值．
考点：利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：（Ⅰ）利用导数求得即可，由f′(x)=3x2-
=3(x2-
)，分a≤0和0＜a＜2两种情况讨论得出单调区间；
（Ⅱ）利用导数法求最大值，注意利用（Ⅰ）的结论．
| 3a |
| 2 |
| a |
| 2 |
（Ⅱ）利用导数法求最大值，注意利用（Ⅰ）的结论．
解答：
解：（Ⅰ）f′(x)=3x2-
=3(x2-
)，…（2分）
当a≤0时，f'（x）≥0，f（x）在[-1，1]上递增； …（3分）
当0＜a＜2时，f（x）在[-1，-
)，(
，1]上递增，在(-
，
)上递减；
…（5分）
当a≥2时，f'（x）≤0，f（x）在[-1，1]上递减． …（6分）
（Ⅱ） 当0＜a＜2时，f（x）在[-1，-
)，(
，1]上递增，在(-
，
)上递减．
f(1)=1-
a+a2=(a-
)2+
＞0，f(-
)=a
+a2＞0，
f(-1)=-1+
a+a2=
(2a-1)(a+2)，f(
)=a2-a
=a
(
-
)．…（9分）
①0＜a＜
时，f（-1）＜0，f(
)＜0，|f(x)|max=max{-f(-1)，f(-
)，-f(
)，f(1)}．
而-f(-1)=1-
a-a2，f(-
)=a
+a2，
-f(
)=-a2+a
，f(1)=1-
a+a2．
显然-f（-1）＜f（1），-f(
)＜f(-
)，
所以只需比较f(-
)与f（1）的大小．f(-
)-f(1)=a
+
a-1．
∵g(a)=a
+
a-1在（0，+∞）上单调递增，而g(
)=0．
∴0＜a＜
时，f(-
)＜f(1)，|f(x)|max=f(1)=1-
a+a2． …（12分）
②
≤a＜2时，f（-1）≥0，f(
)≥0，|f(x)|max=max{f(-
)，f(1)}.f(-
)-f(1)=a
+
a-1≥0，
|f(x)|max=f(-
)=a
+a2…（15分）
综上所述，|f(x)|max=
| 3a |
| 2 |
| a |
| 2 |
当a≤0时，f'（x）≥0，f（x）在[-1，1]上递增； …（3分）
当0＜a＜2时，f（x）在[-1，-
|
|
|
|
…（5分）
当a≥2时，f'（x）≤0，f（x）在[-1，1]上递减． …（6分）
（Ⅱ） 当0＜a＜2时，f（x）在[-1，-
|
|
|
|
f(1)=1-
| 3 |
| 2 |
| 3 |
| 4 |
| 7 |
| 16 |
|
|
f(-1)=-1+
| 3 |
| 2 |
| 1 |
| 2 |
|
|
| a |
| a |
|
①0＜a＜
| 1 |
| 2 |
|
|
|
而-f(-1)=1-
| 3 |
| 2 |
|
|
-f(
|
|
| 3 |
| 2 |
显然-f（-1）＜f（1），-f(
|
|
所以只需比较f(-
|
|
|
| 3 |
| 2 |
∵g(a)=a
|
| 3 |
| 2 |
| 1 |
| 2 |
∴0＜a＜
| 1 |
| 2 |
|
| 3 |
| 2 |
②
| 1 |
| 2 |
|
|
|
|
| 3 |
| 2 |
|f(x)|max=f(-
|
|
综上所述，|f(x)|max=
|
点评：本题考查学生利用导数解决函数的单调区间及最值等综合问题的处理能力，逻辑性较强，属难题，解题时注意分类讨论思想的运用．
练习册系列答案
相关题目
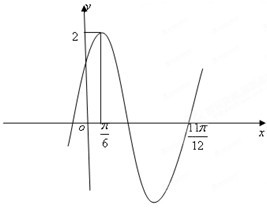已知函数f（x）=Asin（wx+φ）（A＞0，W＞0，|φ|＜
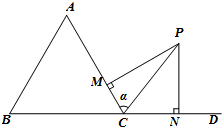设△ABC三个内角A、B、C所对的边分别为a，b，c．已知C=