题目内容
求函数y=
x与y=x-x2围成封闭图形的面积.
| 1 |
| 3 |
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:先联立方程,组成方程组,求得交点坐标,可得被积区间,再用定积分表示出函数y=
x与y=x-x2围成封闭图形的面积,即可求得结论.
| 1 |
| 3 |
解答:
解:由y=
x与y=x-x2联立,可得交点坐标为(0,0),(
,
),
∴函数y=
x与y=x-x2围成封闭图形的面积S=
(x-x2-
x)dx=(
x2-
x3)
=
.
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
∴函数y=
| 1 |
| 3 |
| ∫ |
0 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| | |
0 |
| 4 |
| 81 |
点评:利用定积分求封闭图形的面积是求面积的通法,应熟练掌握.

练习册系列答案
相关题目
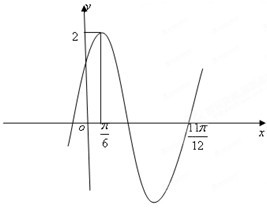 已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<
已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<