题目内容
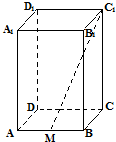如图，正四棱柱（底面是正方形的直棱柱）ABCD-A1B1C1D1的底面边长为1，高为2，M为线段AB的中点，设异面直线CD与MC1所成角为θ，则tanθ=（ ）A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
考点：异面直线及其所成的角
专题：空间角
分析：连结BC1，由CD∥MB，知∠θ=∠C1MB，由此能求出tanθ．
解答：
解：
连结BC1，
∵CD∥MB，∴∠θ=∠C1MB，
∵MB⊥平面BCC1B1，BC1?平面BCC1B1，
∴MB⊥BC1，
由题意知MB=
，BC1=
=
，
∴tanθ=
=
=2
．
故选：C．
连结BC1，∵CD∥MB，∴∠θ=∠C1MB，
∵MB⊥平面BCC1B1，BC1?平面BCC1B1，
∴MB⊥BC1，
由题意知MB=
| 1 |
| 2 |
| 1+4 |
| 5 |
∴tanθ=
| BC1 |
| MB |
| ||
|
| 5 |
故选：C．
点评：本题考查异面直线所成角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力的合理运用．
练习册系列答案
相关题目
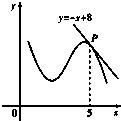如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（ ）A、
| ||
| B、1 | ||
| C、2 | ||
| D、0 |
将4本不同的书分给3个同学，则所有的不同分法种数有（ ）
| A、36 | B、81 | C、64 | D、72 |
已知两条不同的直线l，m和两个不同的平面α，β，则下列命题中：①若l∥m，m?α，则l∥α，②若l∥α，m?α，则l∥m，③若l∥α，l∥β，则α∥β，④若α∥β，l∥α，则l∥β，正确命题个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
若非零实数a，b满足a＜b，则下列不等式正确的是（ ）
| A、a2＜b2 | ||||
| B、a3＜b3 | ||||
| C、|a|＜b | ||||
D、
|
已知向量
=（1，2），
=（2，-3），
=（1，x），若向量
满足
⊥（
+
），则x=（ ）
| a |
| b |
| c |
| c |
| c |
| a |
| b |
| A、4 | B、2 | C、3 | D、6 |