题目内容
已知集合A={x|y=2x+1}，B={y|y=x2+x+1}，则A∩B= ．
考点：交集及其运算
专题：集合
分析：求出A中x的范围确定出A，求出B中y的范围确定出B，找出两集合的交集即可．
解答：
解：由A中y=2x+1，得到A=R，
由B中y=x2+x+1=（x+
）2+
≥
，得到B=[
，+∞），
则A∩B=[
，+∞）．
故答案为：[
，+∞）
由B中y=x2+x+1=（x+
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
则A∩B=[
| 3 |
| 4 |
故答案为：[
| 3 |
| 4 |
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
“自然数中a，b，c恰有一个偶数”的否定为（ ）
| A、自然数a，b，c 都是奇数 |
| B、自然数a，b，c都是偶数 |
| C、自然数a，b，c中至少有两个偶数 |
| D、自然数a，b，c都是奇数或至少有两个偶数 |
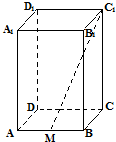如图，正四棱柱（底面是正方形的直棱柱）ABCD-A1B1C1D1的底面边长为1，高为2，M为线段AB的中点，设异面直线CD与MC1所成角为θ，则tanθ=（ ）